The acceleration of a particle is zero as measured from an inertial frame of reference. Can we conclude that no force acts on the particle?
To solve the question, we need to analyze the relationship between force, mass, and acceleration as described by Newton's laws of motion, particularly Newton's first law.
1. Understanding the Given Condition:
The problem states that the acceleration of a particle is zero as measured from an inertial frame of reference. This means that the particle is either at rest or moving with a constant velocity.
2. Applying Newton's First Law:
According to Newton's first law of motion, if a body is at rest or moving with constant velocity, it will continue to do so unless acted upon by a net external force. This implies that if the acceleration is zero, the net force acting on the particle must also be zero.
3. Considering Forces Acting on the Particle:
It is important to note that while the net force is zero, this does not mean that there are no forces acting on the particle. For example, if a block is resting on a surface, the gravitational force (weight) acts downward, and the normal force acts upward. These forces can be equal in magnitude and opposite in direction, resulting in a net force of zero.
4. Conclusion:
Therefore, we cannot conclude that no force acts on the particle simply because its acceleration is zero. There can be multiple forces acting on the particle that balance each other out, leading to a net force of zero and thus zero acceleration.
Final Answer:
No, we cannot conclude that no force acts on the particle. The particle can have forces acting on it that are balanced, resulting in zero net force and zero acceleration.
---
The problem states that the acceleration of a particle is zero as measured from an inertial frame of reference. This means that the particle is either at rest or moving with a constant velocity.
According to Newton's first law of motion, if a body is at rest or moving with constant velocity, it will continue to do so unless acted upon by a net external force. This implies that if the acceleration is zero, the net force acting on the particle must also be zero.
It is important to note that while the net force is zero, this does not mean that there are no forces acting on the particle. For example, if a block is resting on a surface, the gravitational force (weight) acts downward, and the normal force acts upward. These forces can be equal in magnitude and opposite in direction, resulting in a net force of zero.
Therefore, we cannot conclude that no force acts on the particle simply because its acceleration is zero. There can be multiple forces acting on the particle that balance each other out, leading to a net force of zero and thus zero acceleration.
No, we cannot conclude that no force acts on the particle. The particle can have forces acting on it that are balanced, resulting in zero net force and zero acceleration.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions
64 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
Similar Questions
If particle stays at rest as seen from a frame of reference
View SolutionSTATEMENT-1 : Acceleration of a particle in a reference frame may be non- zero , even if net external force acting on the particle is zero.
and
STATEMENT : 2 In a non- - inertial reference frame, Newton's second law is not valid.
View SolutionA particle of mass m is observed from an inertial frame of reference and is found to move in a circle of radius r with a uniform speed v. The centrifugal force on it is
View SolutionA person says that he mesured the acceleration of a particle to be nonzero while no force was acting on the particle
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
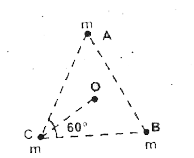
Force acting on particle C, due to particle A and B
View SolutionThe acceleration of a particle is found to be non zero while no force acts on the particle. This is possible if the measurement is made from
View SolutionA constatnt force of 10 N act on a block as shown in figure intal velocity of the particle is zero. It is observed from three frames of reference S1,S2 and ground. The frame S1 start from rest and move with constnat acceleration 10m/s. The frames S1andS2 and particle start moving simultaneously at t=0.
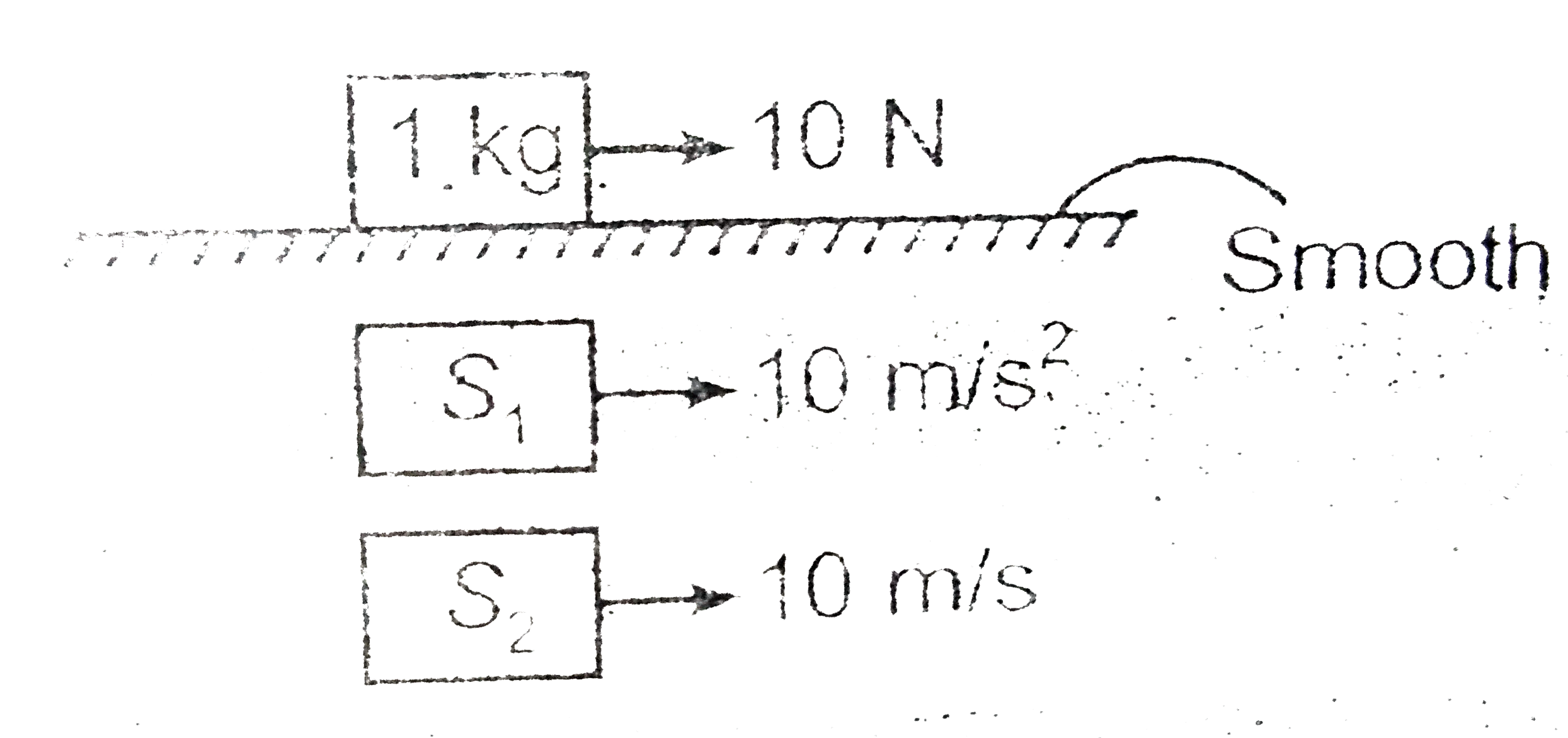
The rate at which work is done by constant force on the particle is always non-negative when observed fom
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
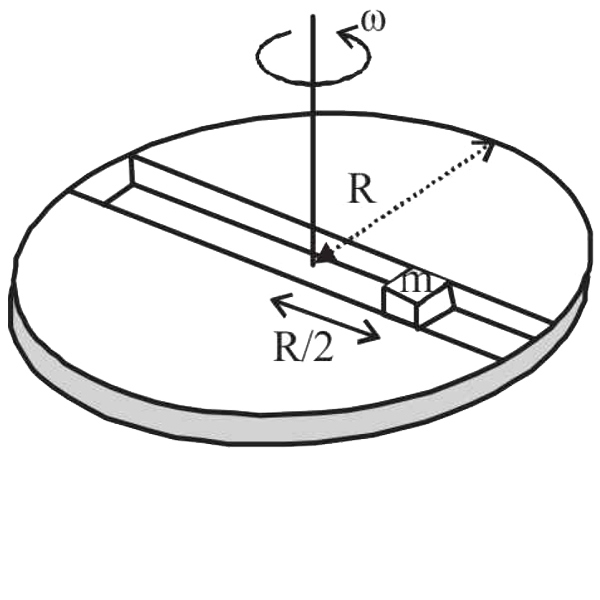
The distance r of the block at time is
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
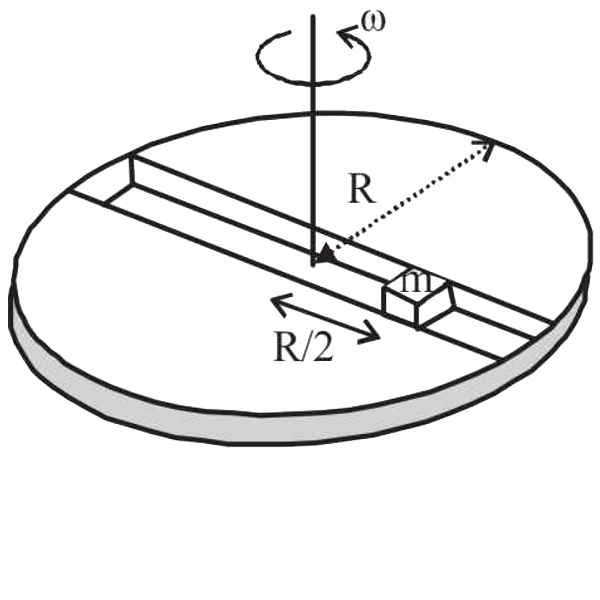
The net reaction of the disc on the block is
View SolutionThe magnetic force depends on →v which depends on the inertial frame of reference. Does then the magnetic force differ from inertial frame to frame? Is it reasonable that the net acceleration has a different value in different frames of reference?
View Solution
