Two particles of masses 1.0 kg and 2.0 kg are placed at a separation of 50 cm. Assuming that the only forces acting on the particles are their mutual gravitation find the initial acceleration of the two particles.
To solve the problem of finding the initial acceleration of two particles due to their mutual gravitational attraction, we can follow these steps:
1. Identify the masses and separation:
- Let mass M=2.0kg (larger mass).
- Let mass m=1.0kg (smaller mass).
- The separation r=50cm=0.5m.
2. Use the formula for gravitational force:
The gravitational force F between two masses is given by Newton's law of gravitation:
F=G⋅M⋅mr2
where G is the universal gravitational constant, G=6.67×10−11N m2/kg2.
3. Substitute the values into the formula:
F=(6.67×10−11)⋅(2.0)⋅(1.0)(0.5)2
F=(6.67×10−11)⋅2.00.25
F=13.34×10−110.25=5.336×10−10N
4. Calculate the acceleration of each mass:
- For mass M (2.0 kg):
aM=FM=5.336×10−102.0=2.668×10−10m/s2
- For mass m (1.0 kg):
am=Fm=5.336×10−101.0=5.336×10−10m/s2
5. Direction of the accelerations:
- The acceleration of mass M is directed towards mass m.
- The acceleration of mass m is directed towards mass M.
Final Answers:
- The acceleration of the 2.0 kg mass is 2.668×10−10m/s2 towards the 1.0 kg mass.
- The acceleration of the 1.0 kg mass is 5.336×10−10m/s2 towards the 2.0 kg mass.
- Let mass M=2.0kg (larger mass).
- Let mass m=1.0kg (smaller mass).
- The separation r=50cm=0.5m.
The gravitational force F between two masses is given by Newton's law of gravitation:
F=G⋅M⋅mr2
where G is the universal gravitational constant, G=6.67×10−11N m2/kg2.
F=(6.67×10−11)⋅(2.0)⋅(1.0)(0.5)2
F=(6.67×10−11)⋅2.00.25
F=13.34×10−110.25=5.336×10−10N
- For mass M (2.0 kg):
aM=FM=5.336×10−102.0=2.668×10−10m/s2
- For mass m (1.0 kg):
am=Fm=5.336×10−101.0=5.336×10−10m/s2
- The acceleration of mass M is directed towards mass m.
- The acceleration of mass m is directed towards mass M.
- The acceleration of the 2.0 kg mass is 2.668×10−10m/s2 towards the 1.0 kg mass.
- The acceleration of the 1.0 kg mass is 5.336×10−10m/s2 towards the 2.0 kg mass.
Topper's Solved these Questions
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - worked out Examples
13 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Objective -1
16 Videos
- FRICTIONBOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Questions for short Answer
11 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
Similar Questions
Three particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
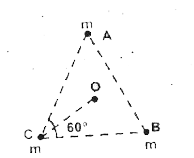
Force acting on particle C, due to particle A and B
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
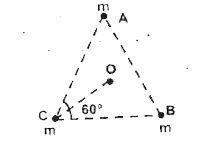
The gravitational potential at O is
View SolutionThree particles, each of the mass m are situated at the vertices of an equilateral triangle of side a. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation a. Find the initial velocity that should be given to each particle and also the time period of the circular motion. (F=Gm1m2r2)
View SolutionThree particles, each of the mass m are situated at the vertices of an equilateral triangle of side a. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation a. Find the initial velocity that should be given to each particle and also the time period of the circular motion. (F=Gm1m2r2)
View SolutionTwo bodies of masses 1 kg and 6×1024 kg are placed with their centres 6.38×106m apart. Calculate the force of attraction between the two masses. Also find the initial acceleration of the two masses. [Assume that no other forces act on them]
View SolutionTwo particles of masses 2m and 3m are placed at separation d on a smooth surface. They move towards each other due to mutual attractive force. Find (a) acceleration of c.m. (b) Velocity of c.m. when separation between particles becomes d/3. ( c) At what distance from the initial position of mass 2m, the particles collide.
View SolutionTwo spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
View SolutionTwo small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational force are acting, find the speeds of the particles when the separation decreases to 0.5 m.
View Solution
