Derive an expression for the gravitational field due to a uniform rod of length L and M at a point on its perpendicular bisector at a distance d from the centre.
The correct Answer is:B, D
A small section of rod is condered at x distance mass of the element
=(ML×dx=dm)
=dE1=G(dm)×1(d2+x2)=dE2
Resultant eE=2dE1sinθ
2×G(dm)d2+x2×d√d2+x2
=2×GM×ddxL(d2+x2({(√d2+x2)})
Total gravitatioN/Al field
E=∫L202GmddxL(d2+x2)32
integrating the above the equation it can be found that
E=2Gmd√L2+4d20
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers18videos
GRAVITATION
- BOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Objective -26videos
GRAVITATION
- BOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Questions for short Answer11videos
FRICTION
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 26videos
HEAT AND TEMPERATURE
Similar Questions
Knowledge Check
- Question 1 - Select One
The radius of gyration of an uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is.
Al√2Bl3Cl√3Dl2
Derive an expression for electric field intensity at a point due to point charge.
View SolutionThe radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
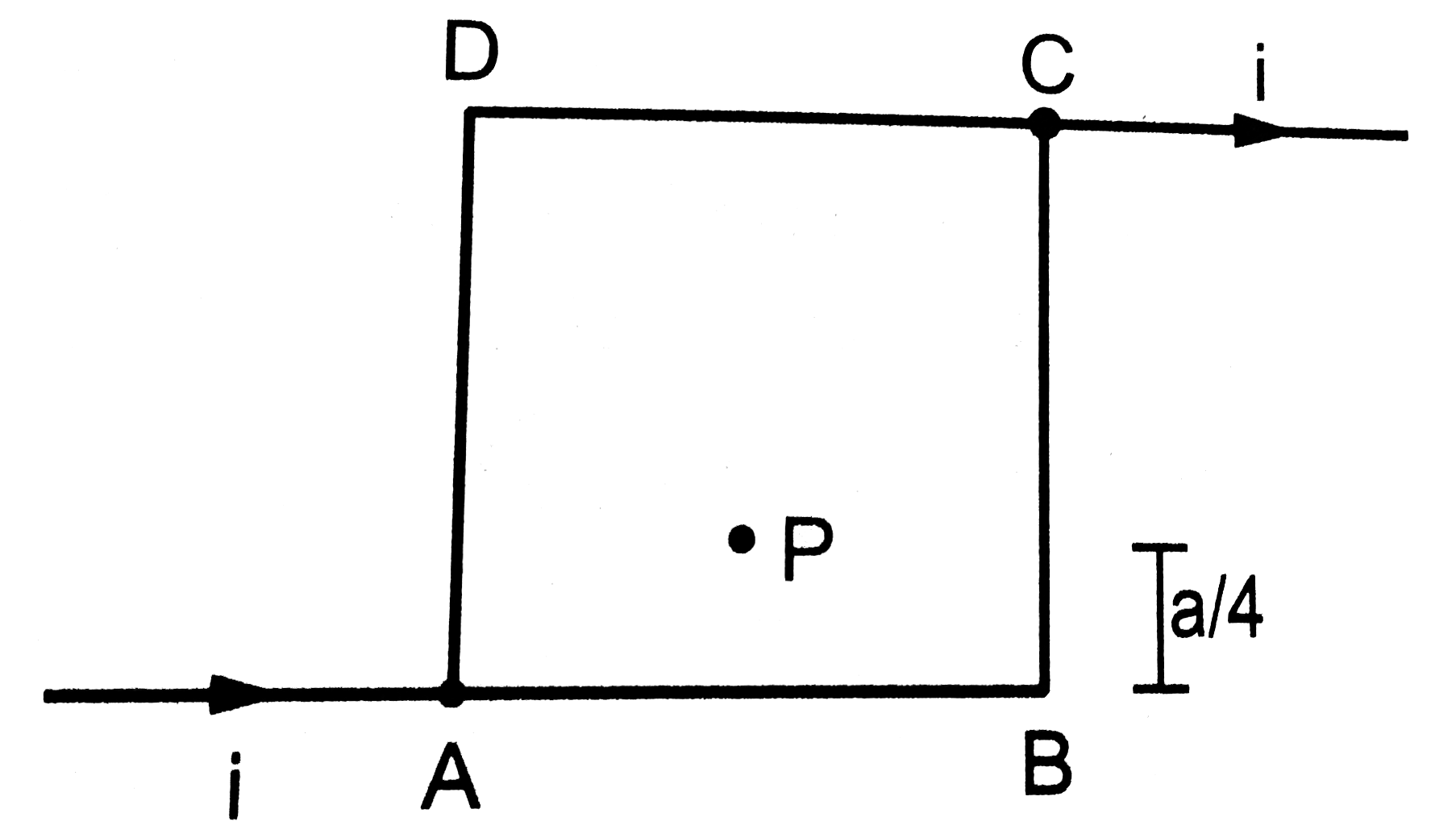
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
 View Solution
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View SolutionCalculate the potential due to a thin charged rod of length L at the points along and perpendicular to the length. Charge per unit length on the rod is λ.
 View Solution
View Solution

