An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one thrid of volume of water was spilled out. The acceleration was
g/3
2g/3
g/2
g/4
The correct Answer is:B
To solve the problem of finding the acceleration of the open cubical tank that spills one-third of its water when accelerated, we can follow these steps:
Step 1: Understand the Problem
We have an open cubical tank filled with water. When the tank is accelerated horizontally, it spills out one-third of its volume of water. We need to find the acceleration of the tank.
Step 2: Define the Variables
Let:
- H = side length of the cube
- V = total volume of water in the tank = H3
- The volume of water spilled = 13V=13H3
Step 3: Determine the Height of the Water Surface
When the tank is accelerated, the water surface will tilt. Let h be the height to which the water surface dips due to acceleration. The volume of the spilled water can be expressed in terms of the height h and the area of the triangle formed by the tilted water surface.
Step 4: Calculate the Volume of Water Spilled
The volume of the spilled water can be calculated as:
Volume of spilled water=Area of triangle×H
The area of the triangle formed by the tilted water surface is:
Area=12×h×H
Thus, the volume of spilled water becomes:
Volume=12×h×H2
Step 5: Set Up the Equation
From the previous steps, we can set up the equation:
13H3=12hH2
Dividing both sides by H2:
13H=12h
Thus, we can express h in terms of H:
h=23H
Step 6: Relate the Angle and Acceleration
The angle θ that the water surface makes with the horizontal can be related to the acceleration a and gravitational acceleration g using:
tanθ=hH
Substituting h:
tanθ=23HH=23
Step 7: Find the Acceleration
Using the relationship tanθ=ag:
ag=23
Thus, the acceleration a can be expressed as:
a=23g
Step 8: Conclusion
The acceleration of the tank is:
2g3
We have an open cubical tank filled with water. When the tank is accelerated horizontally, it spills out one-third of its volume of water. We need to find the acceleration of the tank.
Let:
- H = side length of the cube
- V = total volume of water in the tank = H3
- The volume of water spilled = 13V=13H3
When the tank is accelerated, the water surface will tilt. Let h be the height to which the water surface dips due to acceleration. The volume of the spilled water can be expressed in terms of the height h and the area of the triangle formed by the tilted water surface.
The volume of the spilled water can be calculated as:
Volume of spilled water=Area of triangle×H
The area of the triangle formed by the tilted water surface is:
Area=12×h×H
Thus, the volume of spilled water becomes:
Volume=12×h×H2
From the previous steps, we can set up the equation:
13H3=12hH2
Dividing both sides by H2:
13H=12h
Thus, we can express h in terms of H:
h=23H
The angle θ that the water surface makes with the horizontal can be related to the acceleration a and gravitational acceleration g using:
tanθ=hH
Substituting h:
tanθ=23HH=23
Using the relationship tanθ=ag:
ag=23
Thus, the acceleration a can be expressed as:
a=23g
The acceleration of the tank is:
2g3
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
Knowledge Check
A tank filled with fresh water has a hole in its bottom and water is flowing out of it. If the size of the hole is increased, then
Athe volume of water flowing out per second will decreaseBthe velocity of outflow of water remains unchangedCthe volume of water volume out per second remains zeroDBoth (b) and (c)A closed rectangular tank contains a certain amount of water. When the tank is placed on its 3 ft. by 4 ft. side, the height of the water in the tank is 5 ft. when the tank is placed on another side of dimension 4 ft. by 5 ft., what is the height, in feet, of the surface of the water above the ground?
A2B3C4D5
An open rectangular tank 1.5 m wide 2m deep ad 2 m long is half filled with water. It is accelerated horizontally at 3.27m/s2 in the direction of its length determine the depth of water at each end of tank.
View SolutionA tank if filled with water upto height H. When a hole is made at a distance h below the level of water. What will be the horizontal range of water jet ?
View SolutionA rectangular tank is placed on a horizontal ground and is filled with water to a height H above the base. A small hole is made on one vertical side at a depth D below the level of the water in the tank. The distance x from the bottom of the tank at which the water jet from the tank will hit the ground is
View Solution_E01_226_Q01.png)
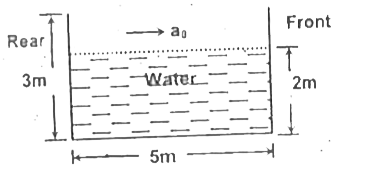
An open retangular tank 5m×4m×3m high containing water upto a height of 2m is accelerated horizontally along the longer side.
(i). Determine the maximum acceleration that can be given without spilling the water.
(ii). Calculate the percentage of water split over if this acceleration of increased by 20%
(iii). If initially the tank is closed at the top and its accelerated horizontally by 9m/s2 find the gauge pressure at the bottom of the front and rear walls of the tank.
View SolutionAn open rectangular tank 5m×4m×3m high containing water upto a height of 2m is accelerated horizontally along the longer side .
(a) Determine the maximum acceleration that can be given without spilling the water .
View SolutionThe water for a factory is stored in a hemispherical tank whose internal diameter is 14 m. The tank contains 50 kL of water. Water is pumped into the tank to fill to its capacity. Calculate the volume of water pumped into the tank.
View Solution