A Young's double slit apparatus has slits separated by 0.28 mm and a screen 48 cm away from the slits. The whole apparatus is immersed in water and the slits are illuminated by the red light (λ=700 nm in vacuum). Find the fringe-width of the pattern formed on the screen.
To solve the problem step by step, we will follow the given information and apply the relevant formulas.
Step 1: Convert the given values to standard units.
1. Distance between the slits (d): Given as 0.28 mm.
d=0.28mm=0.28×10−3m
2. Distance from the slits to the screen (D): Given as 48 cm.
D=48cm=48×10−2m
3. Wavelength of red light in vacuum (λ): Given as 700 nm.
λ=700nm=700×10−9m
Step 2: Calculate the wavelength of light in water.
The refractive index of water (n) is given as 43.
Using the formula for the wavelength in a medium:
λw=λn
Substituting the values:
λw=700×10−943=700×10−9×34=525×10−9m
Step 3: Use the formula for fringe width (β).
The formula for fringe width in Young's double-slit experiment is given by:
β=λw⋅Dd
Substituting the values we have:
β=525×10−9⋅48×10−20.28×10−3
Step 4: Simplify the expression.
Calculating the numerator:
525×48=25200
Now substituting back:
β=25200×10−9×10−20.28×10−3=25200×10−110.28×10−3
Now converting 0.28×10−3 to 2.8×10−4:
β=25200×10−112.8×10−4=252002.8×10−7
Calculating 252002.8:
252002.8=9000
Thus,
β=9000×10−7=0.9×10−3m
Step 5: Convert to millimeters.
β=0.9mm
Final Answer:
The fringe width of the pattern formed on the screen is 0.9 mm.
---
1. Distance between the slits (d): Given as 0.28 mm.
d=0.28mm=0.28×10−3m
D=48cm=48×10−2m
λ=700nm=700×10−9m
The refractive index of water (n) is given as 43.
λw=λn
Substituting the values:
λw=700×10−943=700×10−9×34=525×10−9m
The formula for fringe width in Young's double-slit experiment is given by:
β=λw⋅Dd
β=525×10−9⋅48×10−20.28×10−3
Calculating the numerator:
525×48=25200
Now substituting back:
β=25200×10−9×10−20.28×10−3=25200×10−110.28×10−3
β=25200×10−112.8×10−4=252002.8×10−7
252002.8=9000
Thus,
β=9000×10−7=0.9×10−3m
β=0.9mm
The fringe width of the pattern formed on the screen is 0.9 mm.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Objective -210videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
Similar Questions
A Young's double slit apparatus has slits separated by 0.25mm and a screen 48cm away from the slits. The whole apparatus is immersed in water and the slits are illuminated by the red light (λ=700nm in vacuum.) Find the fringe width of the pattern formed on the screen. (μw=4/3)
View SolutionIf Young.s double slit apparatus is shifted from air to water, then
View SolutionIn a Young's double slit experiment , the slits are Kept 2mm apart and the screen is positioned 140cm away from the plane of the slits. The slits are illuminatedd with light of wavelength 600nm. Find the distance of the third brite fringe. From the central maximum . in the interface pattern obtained on the screen frings from the central maximum. 3
View SolutionIn a Young's double slit experiment, the slit separation is 1mm and the screen is 1m from the slit. For a monochromatic light of wavelength 500nm, the distance of 3rd minima from the central maxima is
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View SolutionIn a Young's double-slit experiment , the slits are separated by 0.28 mm and screen is placed 1.4 m away . The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm . Determine the wavelength of light used in the experiment .
View SolutionIn a Young's double-slit experiment , the slits are separated by 0.28 mm and screen is placed 1.4 m away . The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm . Determine the wavelength of light used in the experiment .
View SolutionIn Young's double-slit experiment, the slit separation is 0.5 mm and the screen is 0.5 m away from the slit. For a monochromatic light of wavelength 500 nm, the distance of 3rd maxima from the 2nd minima on the other side of central maxima is
View SolutionTwo slits, 4 mm apart, are illuminated by light of wavelength 6000Å. What will be the fringe width on a screen placed 2 m from the slits
View SolutionA double slit S1−S2 is illuminated by a coherent light of wavelength λ. The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1, from it and a screen ∑ is placed behind the double slit at a distance D2, from it . The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
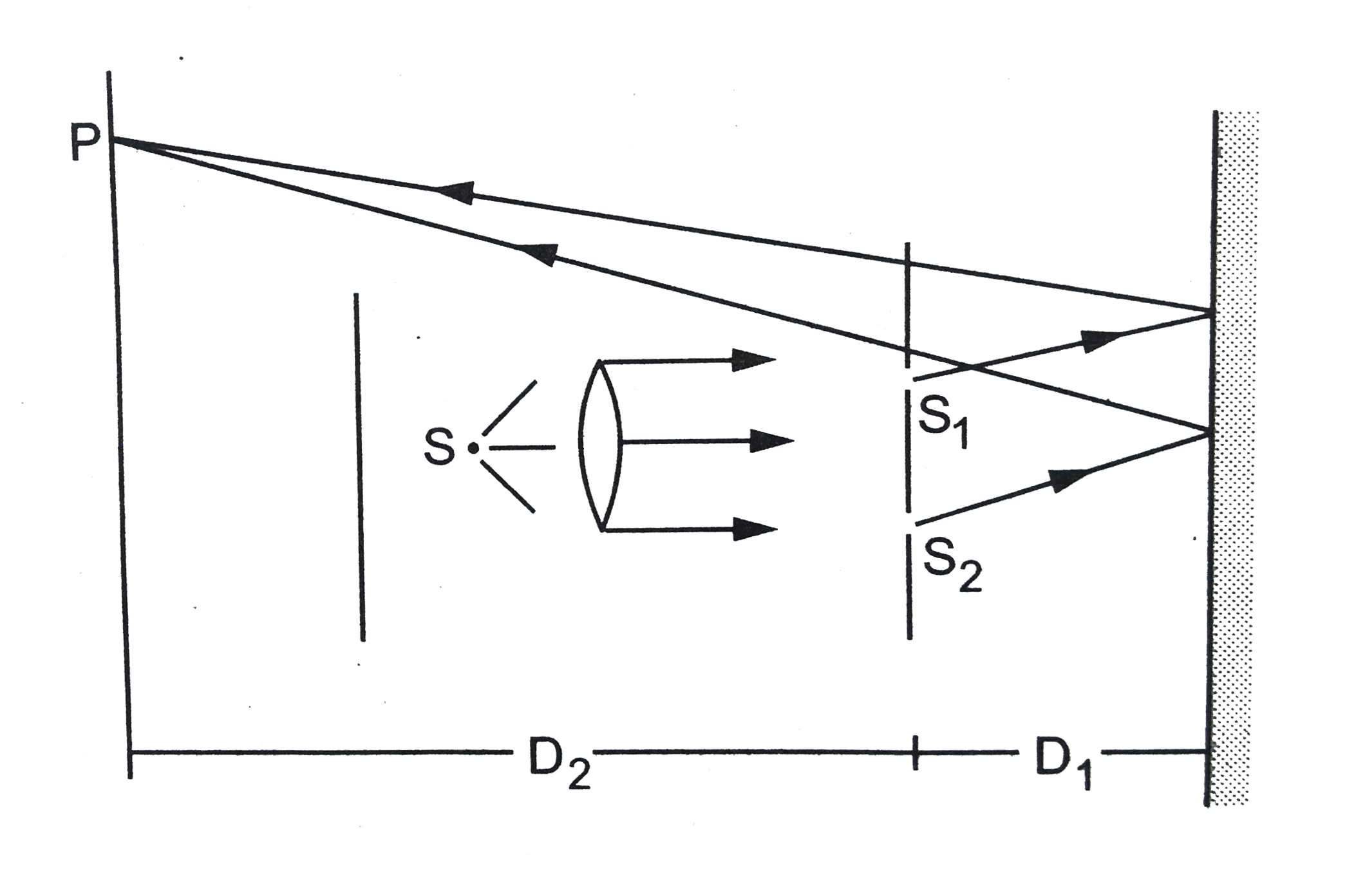 View Solution
View Solution

