Question

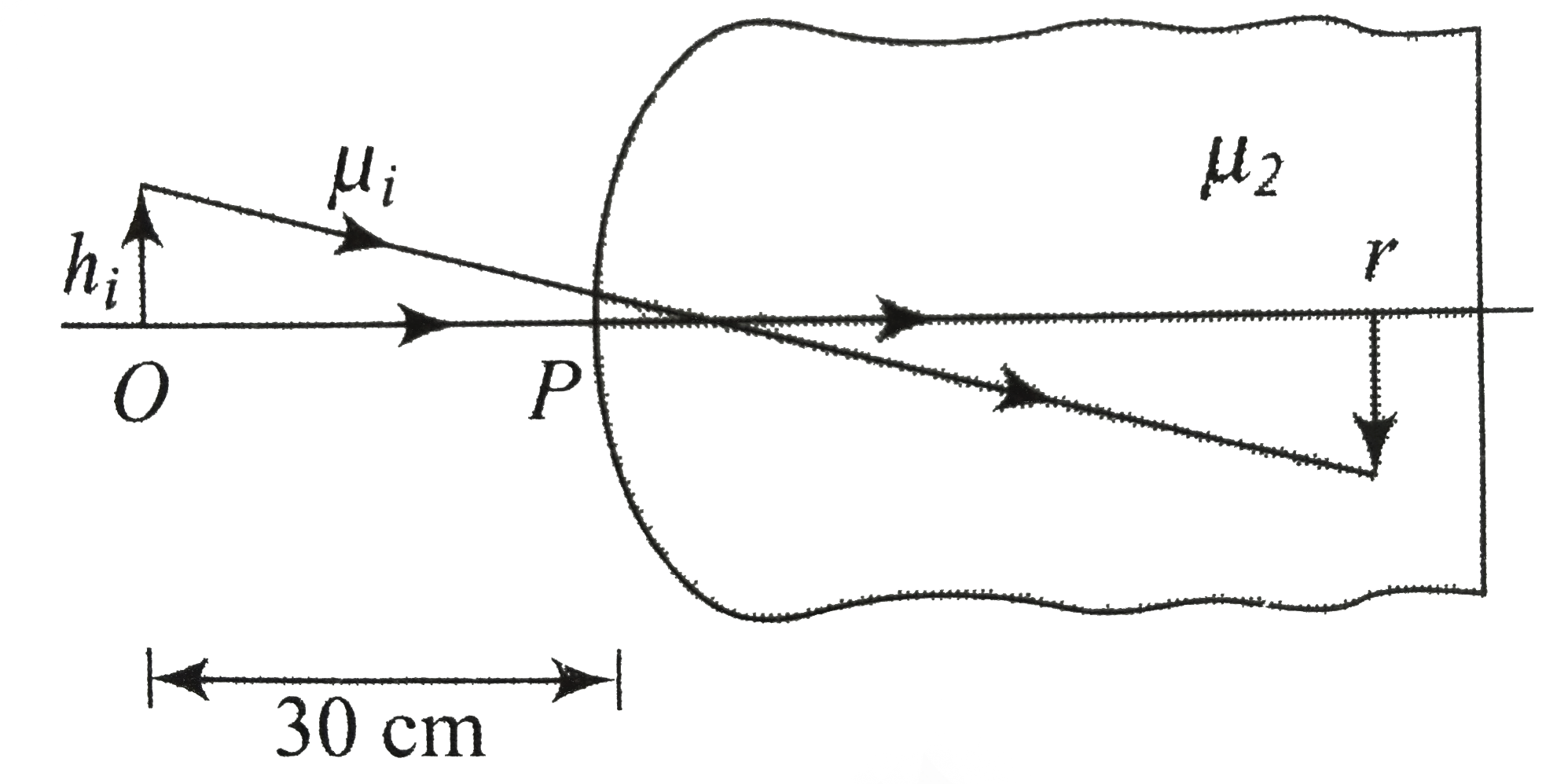
A small object is embedded in a glass sphere (mu =1.5) of radius 5.0 cm at a distance 1.5 cm left to the centre. Locate the image of the object as seen by an observer standing (a) to the left of the sphere and (b) to the right of the sphere.

Answer

A::B::C

Explanation

To solve the problem of locating the image of a small object embedded in a glass sphere, we will follow these steps:

Step 1: Understand the Setup
- We have a glass sphere with a refractive index (μ) of 1.5 and a radius (R) of 5.0 cm.
- The object is located 1.5 cm to the left of the center of the sphere.

Step 2: Determine Object Distance
- The center of the sphere is taken as the origin (0 cm).
- The object is located at -1.5 cm (1.5 cm to the left of the center).
- The radius of the sphere is 5 cm, so the object distance (u) from the surface of the sphere is:
\( u = R - 1.5 = 5.0 - 1.5 = 3.5 \text{ cm} \)
Since the object is to the left of the center, we take u as negative:
\( u = -3.5 \text{ cm} \)

Step 3: Apply the Refraction Formula
- We will use the formula for refraction at a spherical surface:
\( \frac{\mu_1}{v} - \frac{\mu_2}{u} = \frac{\mu_1 - \mu_2}{R} \)
Here,
- μ1 (air) = 1,
- μ2 (glass) = 1.5,
- R = -5 cm (since the surface is bulging inwards).

Step 4: Substitute Values for the Left Observer
- Substitute the values into the formula:
\( \frac{1}{v} - \frac{1.5}{-3.5} = \frac{1 - 1.5}{-5} \)
Simplifying gives:
\( \frac{1}{v} + \frac{1.5}{3.5} = \frac{-0.5}{-5} \)
\( \frac{1}{v} + \frac{3}{7} = \frac{1}{10} \)

Step 5: Solve for v
- Rearranging gives:
\( \frac{1}{v} = \frac{1}{10} - \frac{3}{7} \)
Finding a common denominator (70):
\( \frac{1}{v} = \frac{7}{70} - \frac{30}{70} = -\frac{23}{70} \)
Thus,
\( v = -\frac{70}{23} \approx -3.04 \text{ cm} \)
- This indicates that the image is formed 3.04 cm to the left of the surface of the sphere.

Step 6: Repeat for the Right Observer
- For the observer on the right side, the object distance will be:
\( u = 5 + 1.5 = 6.5 \text{ cm} \quad \text{(still negative)} \)
So,
\( u = -6.5 \text{ cm} \)

Step 7: Substitute Values for the Right Observer
- Again using the refraction formula:
\( \frac{1}{v} - \frac{1.5}{-6.5} = \frac{1 - 1.5}{-5} \)
Simplifying gives:
\( \frac{1}{v} + \frac{1.5}{6.5} = \frac{-0.5}{-5} \)
\( \frac{1}{v} + \frac{3}{13} = \frac{1}{10} \)

Step 8: Solve for v Again
- Rearranging gives:
\( \frac{1}{v} = \frac{1}{10} - \frac{3}{13} \)
Finding a common denominator (130):
\( \frac{1}{v} = \frac{13}{130} - \frac{30}{130} = -\frac{17}{130} \)
Thus,
\( v = -\frac{130}{17} \approx -7.65 \text{ cm} \)
- This indicates that the image is formed 7.65 cm to the left of the surface of the sphere.

Final Results
- (a) The image as seen by an observer to the left of the sphere is approximately 3.04 cm to the left of the surface.
- (b) The image as seen by an observer to the right of the sphere is approximately 7.65 cm to the left of the surface.