Conside the situation shown in figure. The frame is made of the same material and has a unifrom cross-section area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at 100∘C is 130J .
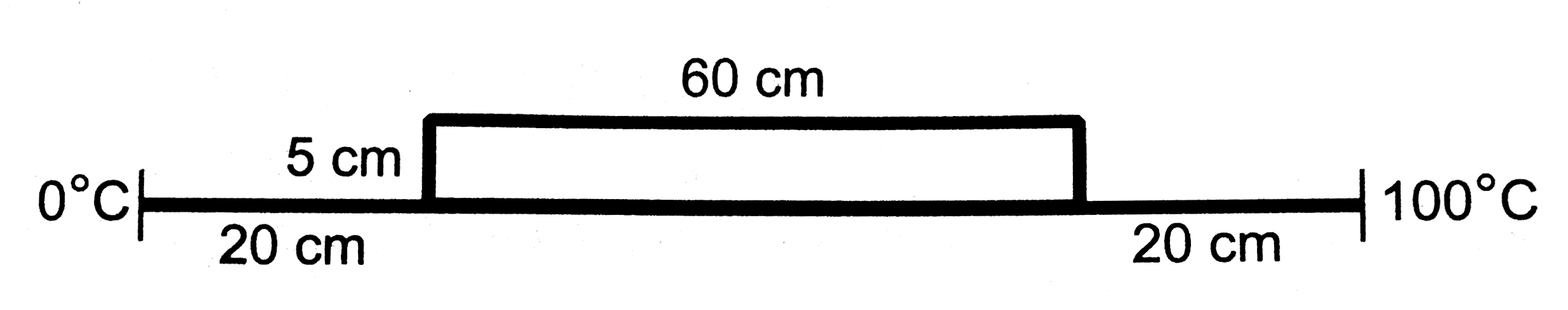
(Q/t)_(AB)=(Q/t)_(Bent)+(Q/t)_(Straight)<br>(Q/t)_(Bent)=(KA(theta_1-theta_2))/(70)<br>(Qt)Straight=KA(θ1−θ2)60
(Qt)Bent(Qt)straight=6070=67
⇒(Qt)Bent+(Qt)Straight=130
(Qt)Bent+(Qt)Bent×76=130
⇒((76)+1)(Qt)Bent=130
⇒136×(Qt)Bent=130
(Qt)Bent=130×613=60J/s.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER11videos
HEAT TRANSFER
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - OBJECTIVE II6videos
HEAT TRANSFER
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 26videos
HEAT AND TEMPERATURE
- BOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer4videos
INTRODUCTION TO PHYSICS
Similar Questions
Find the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1) . Thermal conductivity of the material of the rod is K.
 View Solution
View SolutionA rod is made of uniform material and has non-uniform cross section. It is fixed at both the ends as shown and heated at mid-section. Which of the following are not correct?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A rectangular coil of 20 turns and area of cross-section 25cm2 has a resistance of 100ohm. If a magnetic field which is perpendicular to the plane of the coil changes at the rate of 1000 telsa per second, the current in the coil is
A1AB50 AC0.5AD5A
A semicircular rods is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross section of the straight rod in a given time.
View SolutionThe circuit in figure is made of a homogeneous wire of uniform cross-section. 1234 is a square. Find the ratio Q12/Q34 of the amounts of heat liberated per unit time in conductor 1-2 and 3-4
 View Solution
View SolutionTwo rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.
 View Solution
View SolutionThree rods are made from the same material and having the same cross-sectional area and length have been joined as shown in the figure.
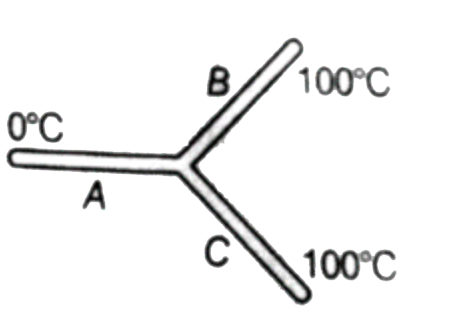
The left end and right end are kept 0∘Cand100∘C , respectively . The temperature of the junction of three rods will beView SolutionAn irregular rod of same uniform material as shown in figure is conducting heat at a steady rate. The temperature gradient at various sections versus area of cross section graph will be
_S01_094_Q01.png) View Solution
View SolutionConsidering a wire of non-uniform cross-section as shown.If the area of cross-section at A is double of the area of cross-section at point B.Ratio of heat energy dissipated in a unit volume per unit time at points A and B is
_PHY_E05_279_Q01.png) View Solution
View SolutionThree conducting rods of same material and cross-section are shown in figure. Temperatures of A,D and C are maintained at 20∘C,90∘Cand0∘C. The ratio of lengths BD and BC if there is no heat flow in AB is
 View Solution
View Solution

