A voltmeter coil has resistance 50.0(Ω)and a resistor of 1.15k(Ω)is connected in series.It can read potential differences upto 12 volts.If this same coil is used to construct an ammeter which can measure currents up to 2.0A ,What should be the resistance of the shunt used ?
To solve the problem step by step, we will follow these calculations:
Step 1: Determine the Effective Resistance of the Voltmeter
The voltmeter coil has a resistance of Rv=50Ω and a series resistor of Rs=1.15kΩ=1150Ω.
The effective resistance Reff of the voltmeter is given by:
Reff=Rv+Rs=50Ω+1150Ω=1200Ω
Step 2: Calculate the Maximum Current through the Voltmeter
The voltmeter can read a maximum potential difference of V=12V.
Using Ohm's law, the maximum current Imax that the voltmeter can sustain is:
Imax=VReff=12V1200Ω=0.01A
Step 3: Set Up the Ammeter Configuration
To construct an ammeter, we will connect a shunt resistor R in parallel with the voltmeter coil (50 Ω).
The total current Itotal that the ammeter can measure is given as 2.0A.
The current through the voltmeter coil (which we calculated earlier) is Iv=0.01A.
Step 4: Calculate the Current through the Shunt Resistor
The current through the shunt resistor IR can be calculated as:
IR=Itotal−Iv=2.0A−0.01A=1.99A
Step 5: Apply the Voltage Drop Condition
Since the voltmeter coil and the shunt resistor are in parallel, the voltage drop across both is the same.
Using Ohm's law for both resistors:
V=Iv⋅Rv=IR⋅R
Substituting the known values:
0.01A⋅50Ω=1.99A⋅R
Step 6: Solve for the Shunt Resistance R
Rearranging the equation gives:
R=0.01⋅501.99
Calculating this:
R=0.51.99≈0.2513Ω
Final Answer
Thus, the resistance of the shunt used should be approximately:
R≈0.251Ω
---
The voltmeter coil has a resistance of Rv=50Ω and a series resistor of Rs=1.15kΩ=1150Ω.
Reff=Rv+Rs=50Ω+1150Ω=1200Ω
The voltmeter can read a maximum potential difference of V=12V.
Imax=VReff=12V1200Ω=0.01A
To construct an ammeter, we will connect a shunt resistor R in parallel with the voltmeter coil (50 Ω).
The current through the shunt resistor IR can be calculated as:
IR=Itotal−Iv=2.0A−0.01A=1.99A
Since the voltmeter coil and the shunt resistor are in parallel, the voltage drop across both is the same.
V=Iv⋅Rv=IR⋅R
Substituting the known values:
0.01A⋅50Ω=1.99A⋅R
Rearranging the equation gives:
R=0.01⋅501.99
Calculating this:
R=0.51.99≈0.2513Ω
Thus, the resistance of the shunt used should be approximately:
R≈0.251Ω
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer17videos
ELECTRIC CURRENT IN CONDUCTORS
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 29videos
ELECTRIC CURRENT IN CONDUCTORS
- BOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer6videos
DISPERSION AND SPECTRA
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer6videos
ELECTRIC CURRENT THROUGH GASES
Similar Questions
An ammeter is to be constructed which can read currents up to 2.0A. If the coil has a resistance of 25(Ω)and takes 1mA for full-scale deflection, what should be the resistance of the shunt used?
View SolutionAn ammeter of resistance 0⋅80Ω can measure current upto 1⋅0A.
(a) What must be the value of shunt resistance to enable the ammeter to measure current upto 5⋅0A?
(b) What is the combined resistance of the ammeter and the shunt?View SolutionA coil having a resistance of 50.0Ω and an inductance of 0.500 henry is connected to an AC source of 110 volts, 50.0 cycle/s. Find the rms value of the current in the circuit.
View SolutionA galvanometer coil has a resistance 90Ω and full scale deflection current 10mA. A 910Ω resistance is connected in series with the galvanometer to make a voltmeter. If the least count of the voltmeter is 0.1V the number of divisions on its scale is
View SolutionTo the potentiometer wire of L and 10Ω resistance, a battery of emf 2.5 volts and a resistance R are connected in series. If a potential difference of 1 volt is balanced across L/2 length, the value of R is Ω will be
View SolutionAn ammeter of resistance 0.6Ω can measure current upto 1.0 A. Calculate (i) The shunt resistance required to enable the ammeter to measure current upto 5.0 A (ii) The combined resistance of the ammeter and the shunt.
View SolutionThe resistance of an ammeter is 13Ω and its scale is graduated for a current upto 100A. After an additional shunt has been connected to this ammeter it becomes possible to measure currents upto 750A by this meter. The value of shunt resistance is
View SolutionResistance R1and R2, each 60Ω, are connected in series. The Potential difference between points A and B is 120V. Find the reading of voltmeter connected resistance r=120Ω
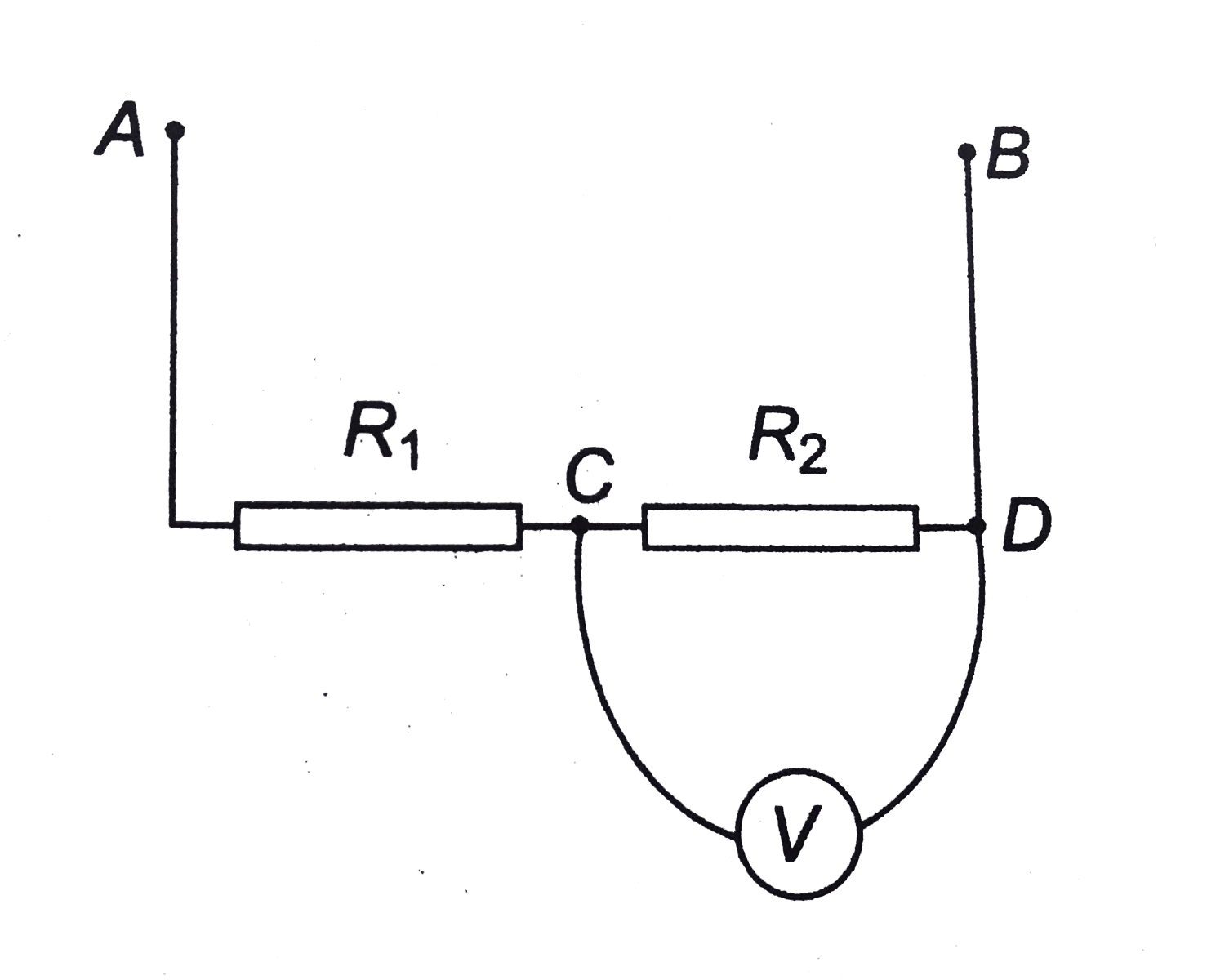 View Solution
View SolutionAn ammeter of resistance 1 Ohm can measure current upto 1.0 A. (i) What must be the value of the shunt resistance to enable the ammeter to measure upto 5.0 A? (ii) What is the combined resistance of the ammeter and the shunt?
View SolutionA galvanometer with its coil resistance 25Ω requires a current of 1 mA for its full deflection. In order to construct an ammeter to read up to a current of 2A, the approximate value of the shunt resistance should be :
View Solution

