Suppose the resistance of the coil in the previous problem is 25Ω. Assume that the coil moves with uniform velocity during its removal and restoration. Find the thermal energy developed in the coil during (a) its removal, (b) its restoration and (c) its motion.
To solve the problem, we need to calculate the thermal energy developed in the coil during three different scenarios: (a) its removal from the magnetic field, (b) its restoration back into the magnetic field, and (c) during its motion.
Given Data:
- Resistance of the coil, R=25Ω
- Length of each side of the square coil, l=0.5m (50 cm)
- Number of turns, N=50
- Magnetic field strength, B=1T
- Time taken for removal and restoration, t=0.25s
Step 1: Calculate the magnetic flux when the coil is fully inside the magnetic field.
The area A of the square coil is given by:
A=l×l=0.5m×0.5m=0.25m2
The magnetic flux Φ when the coil is fully inside the magnetic field is:
Φ=B×A×N=1T×0.25m2×50=12.5Wb
Step 2: Calculate the average EMF induced during the removal of the coil.
When the coil is removed, the final flux Φ2=0 (since it is out of the magnetic field). The change in flux ΔΦ is:
ΔΦ=Φ1−Φ2=12.5Wb−0=12.5Wb
The average EMF E induced is given by:
E=−ΔΦΔt=−12.5Wb0.25s=−50V
(The negative sign indicates the direction of the induced EMF, but we are interested in the magnitude.)
Step 3: Calculate the current in the coil during removal.
Using Ohm's law, the current I is given by:
I=ER=50V25Ω=2A
Step 4: Calculate the thermal energy developed during the removal of the coil.
The thermal energy Q developed can be calculated using:
Q=I2Rt
Substituting the values:
Q=(2A)2×25Ω×0.25s=4×25×0.25=25J
Step 5: Calculate the thermal energy developed during the restoration of the coil.
The situation during restoration is similar to removal. The induced EMF and current will be the same:
E=50V,I=2A
Thus, the thermal energy developed during restoration is also:
Q=I2Rt=(2A)2×25Ω×0.25s=25J
Step 6: Calculate the total thermal energy developed during the motion of the coil.
The total thermal energy developed during the motion (removal + restoration) is:
Qtotal=Qremoval+Qrestoration=25J+25J=50J
Final Answers:
(a) Thermal energy during removal: 25 J
(b) Thermal energy during restoration: 25 J
(c) Total thermal energy during motion: 50 J
- Resistance of the coil, R=25Ω
- Length of each side of the square coil, l=0.5m (50 cm)
- Number of turns, N=50
- Magnetic field strength, B=1T
- Time taken for removal and restoration, t=0.25s
The area A of the square coil is given by:
A=l×l=0.5m×0.5m=0.25m2
The magnetic flux Φ when the coil is fully inside the magnetic field is:
Φ=B×A×N=1T×0.25m2×50=12.5Wb
When the coil is removed, the final flux Φ2=0 (since it is out of the magnetic field). The change in flux ΔΦ is:
ΔΦ=Φ1−Φ2=12.5Wb−0=12.5Wb
The average EMF E induced is given by:
E=−ΔΦΔt=−12.5Wb0.25s=−50V
(The negative sign indicates the direction of the induced EMF, but we are interested in the magnitude.)
Using Ohm's law, the current I is given by:
I=ER=50V25Ω=2A
The thermal energy Q developed can be calculated using:
Q=I2Rt
Substituting the values:
Q=(2A)2×25Ω×0.25s=4×25×0.25=25J
The situation during restoration is similar to removal. The induced EMF and current will be the same:
E=50V,I=2A
Thus, the thermal energy developed during restoration is also:
Q=I2Rt=(2A)2×25Ω×0.25s=25J
The total thermal energy developed during the motion (removal + restoration) is:
Qtotal=Qremoval+Qrestoration=25J+25J=50J
(a) Thermal energy during removal: 25 J
(b) Thermal energy during restoration: 25 J
(c) Total thermal energy during motion: 50 J
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 27videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
Similar Questions
A square- shaped copper coil has edges of length 50cm and contains 50 turns. It is placed perpendicular to 1.0 T magnetic field. It is removed form the magnetic field in 0.25 s and restored in its joriginal place in the next 0.25 s. Find the magnitude of the average emf induced in the loop during (a) its removal, (b) its restoration and (c) its motion.
View SolutionA particle moves with constant angular velocity in a circle. During the motion its
View Solutionsuppose the ends of the coil in the previous problem are connected to a resistane of 100Ω. Neglecting the resistance of the coil, find the heat produced in the circuit in one minute.
View SolutionA wheel of mass 1.4 kg and radius 0.4 m is mounted on a frictionless, horizontal axle as shown in Fig. 7.2.50. Alight string wrapped around the rim supports a mass of 2 kg. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ? Also find the tension in the string.
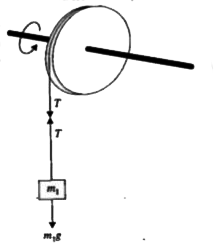 View Solution
View SolutionWhat would be the energy of the magnetic field of the coil of the previous problem, if its core were of a nonferromagnetic material? What is the source of oxcess energy in the case of a ferromagnetic core?
View SolutionA planar coil having 12 turns carries 15 A current. The coil is oriented with respect to the uniform magnetic field B=0.2ˆiT such that its directed area is A=0.04ˆim2. the potential energy of the coil in the given orientation is
View SolutionA closed coil having 100 turns is rotated in a uniform magnetic field B=4.0X10−4 T about a diameter which is perpendicular to the field. The angular velocity of rotation is 300 revolutions per minute. The area of the coil is 25cm2 and its resistance is 4.0Ω. Find (a) the average emf developed in the half a turn form a position where the coil is perpendicular to the magnetic field, (b) the average emf in a full turn and (c) the net charge displaced in part (a).
View SolutionA ball is released from point A. During its motion ball takes two seconds from B to C Find the time taken by ball from A to C.
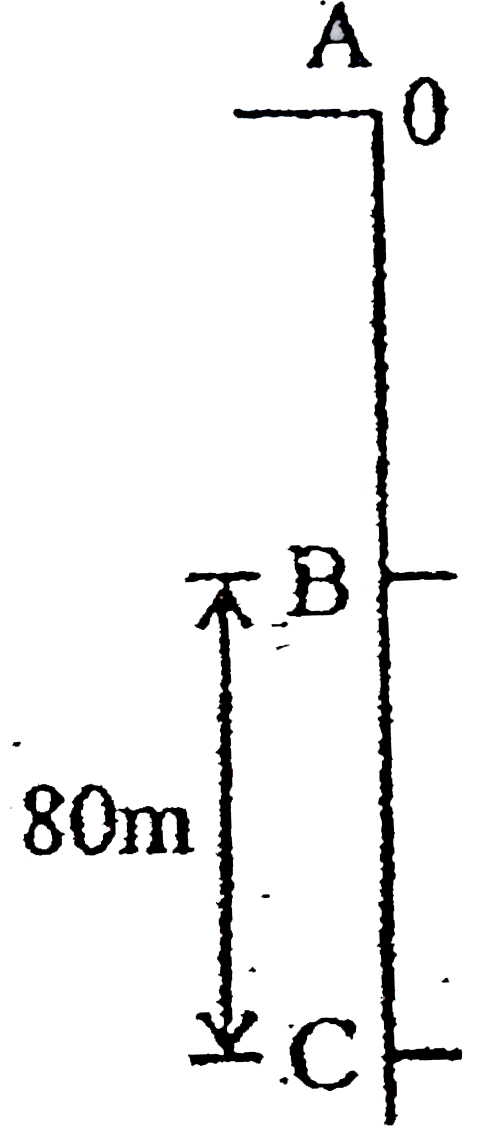 .View Solution
.View SolutionA body moving with uniform acceleration a straight line describes 25m in the fifth second and 33m in the seventh second. Find its initial velocity and acceleration.
View SolutionA circular loop of radius 1m is placed in a varying magnetic field given as B=6t Tesla, where t is time in sec.
(a)Find the emf induced in the coil if the plane of the coil is perpendicular to the magnetic field.
(b) Find the electric field in the tangential directin, induced due to the changing magnetic field.
(c)Find the current in the loop if its resistance is 1Ω/m.View Solution

