In a series lags the applied emf. The rate at which energy is dissipated in the resistor, can be increased by
Decreasing the capacitance and making no other change
Increasing the capacitance and making no other change
Increasing the inductance and making no other change
Increasing the driving frequency and making no other change
The correct Answer is:A
To solve the problem of how to increase the rate at which energy is dissipated in a resistor in a series LCR circuit where the current lags the applied emf, we can follow these steps:
Step 1: Understand the Power Dissipation in a Resistor
The power dissipated in a resistor (P) in an AC circuit can be expressed as:
P=I2R
where I is the current through the resistor and R is the resistance.
Step 2: Identify Factors Affecting Current
The current in an LCR circuit is affected by the impedance (Z) of the circuit, which is given by:
Z=√R2+(XL−XC)2
where:
- XL=ωL (inductive reactance)
- XC=1ωC (capacitive reactance)
- ω is the angular frequency of the AC source.
Step 3: Analyze the Given Options
We need to analyze how each option affects the impedance and thus the current:
1. Decreasing the Capacitance (C):
- If capacitance C decreases, XC increases (since XC=1ωC).
- This results in XL−XC decreasing, which leads to a decrease in impedance Z.
- Since I=VZ, a decrease in Z results in an increase in current I.
- Thus, power P=I2R increases.
2. Increasing the Capacitance (C):
- If capacitance C increases, XC decreases.
- This results in XL−XC increasing, which leads to an increase in impedance Z.
- This results in a decrease in current I, thus decreasing power P.
3. Increasing the Inductance (L):
- If inductance L increases, XL increases.
- This results in XL−XC increasing, which leads to an increase in impedance Z.
- This results in a decrease in current I, thus decreasing power P.
4. Increasing the Driving Frequency (ω):
- If frequency ω increases, XL increases and XC decreases.
- The net effect on XL−XC depends on the relative rates of change, but typically leads to an increase in impedance Z.
- This results in a decrease in current I, thus decreasing power P.
Conclusion
From the analysis, the only option that increases the power dissipation in the resistor is:
Decreasing the capacitance and making no other changes.
Final Answer
The rate at which energy is dissipated in the resistor can be increased by decreasing the capacitance and making no other changes.
---
The power dissipated in a resistor (P) in an AC circuit can be expressed as:
P=I2R
where I is the current through the resistor and R is the resistance.
The current in an LCR circuit is affected by the impedance (Z) of the circuit, which is given by:
Z=√R2+(XL−XC)2
where:
- XL=ωL (inductive reactance)
- XC=1ωC (capacitive reactance)
- ω is the angular frequency of the AC source.
We need to analyze how each option affects the impedance and thus the current:
- If capacitance C decreases, XC increases (since XC=1ωC).
- This results in XL−XC decreasing, which leads to a decrease in impedance Z.
- Since I=VZ, a decrease in Z results in an increase in current I.
- Thus, power P=I2R increases.
- If capacitance C increases, XC decreases.
- This results in XL−XC increasing, which leads to an increase in impedance Z.
- This results in a decrease in current I, thus decreasing power P.
- If inductance L increases, XL increases.
- This results in XL−XC increasing, which leads to an increase in impedance Z.
- This results in a decrease in current I, thus decreasing power P.
- If frequency ω increases, XL increases and XC decreases.
- The net effect on XL−XC depends on the relative rates of change, but typically leads to an increase in impedance Z.
- This results in a decrease in current I, thus decreasing power P.
From the analysis, the only option that increases the power dissipation in the resistor is:
The rate at which energy is dissipated in the resistor can be increased by decreasing the capacitance and making no other changes.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - B) (Objective Type Questions (One option is correct))
14 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - C ) (Objective Type Questions) ( More than one option are correct)
2 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Try Yourself
15 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION J (Aakash Challengers )
5 Videos
Similar Questions
Consider the RL circuit in Fig. When the switch is closed in position 1 and opens in position 2, electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of PL/PR of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio PL/PR as a function of time.
c. If the time constant of circuit is t, what is the time at which PL=PR?
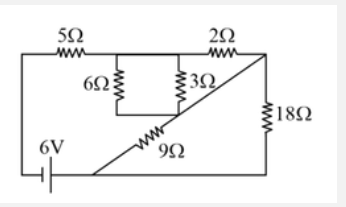
View SolutionFind the resistor in which the dissipated power is the greatest -
View SolutionA car battery with a 12V e.m.f. and an internal resistance of 0.04Ω is being charged with a current of 50A.
The rate at which energy is being dissipated as heat inside the battery is:
View SolutionIf a battery of emf E and internal resistance r is connected across a load of resistance R. Shot that the rate at which energy is dissipated in R is maximum when R=r and this maximur power is P=E2/4r.
View SolutionA 20 H inductor is placed in series with 10 W resistor and an emf of 100 V is suddenly applied to the combination. At t = 1 s from t = 1 s from the start, find the rate at which energy is being stored in the magnetic field around the inductor (givne e−0.5=0.61).
View SolutionThe switch shown in figure is suddenly closed. Find the current through the resistor when energy dissipated in the resistor is one third of total energy dissipated in the resistor.

View SolutionAn inducatane L and a resistance R are connected in series with a battery of emf epsilon. Find the maximum rate at which the energy is stored in the magnetic field.
View SolutionAn LR series circuit has L=1H and R=1Ω.It is connected across an emf of 2V.The maximum rate at which energy is stored in the magnetic field is:

View SolutionAn inductor 2/π Henry, a capacitor 100/TμF and a resistor 75Ω are connected in series across a source of emf V=10sin100πt. Here t is in second. (a) find the impedance of the circuit. (b) find the energy dissipated in the circuit in 20 minutes.
View SolutionDaniel cell, the EMF of the cell can b e increased b y
View Solution