Three charges +Q, q, +Q are placed respectively, at distance, 0, d//2 and d from the origin, on the x-axis. If the net force experienced by +Q placed at x=0, is zero, then value of q is :
To solve the problem, we need to analyze the forces acting on the charge +Q placed at the origin (x = 0) due to the other two charges +Q (at x = d) and q (at x = d/2).
1. Identify the Charges and Their Positions:
- Charge +Q is at x = 0.
- Charge +Q is at x = d.
- Charge q is at x = d/2.
2. Determine the Forces Acting on Charge +Q at x = 0:
- The charge at x = d will exert a repulsive force on the charge at the origin (since both are positive).
- The charge at x = d/2 will also exert a force on the charge at the origin. The nature of this force will depend on the sign of charge q.
3. Assume the Sign of Charge q:
- If q is positive, it will repel the charge at the origin, adding to the force from the charge at x = d.
- If q is negative, it will attract the charge at the origin, opposing the repulsive force from the charge at x = d.
4. Set Up the Force Equations:
- The force due to the charge at x = d on the charge at x = 0 is given by:
F+Q=kQ⋅Qd2=kQ2d2
- The force due to the charge q at x = d/2 on the charge at x = 0 is given by:
Fq=kQ⋅q(d/2)2=k4Qqd2
5. Set the Net Force to Zero:
- For the net force on the charge at x = 0 to be zero, the attractive force from charge q must balance the repulsive force from the charge at x = d:
k4Qqd2=kQ2d2
- We can cancel out k and d2 from both sides:
4Qq=Q2
6. Solve for q:
- Rearranging gives:
q=Q24Q=Q4
- Since we assumed q must be negative for the forces to balance, we conclude:
q=−Q4
Final Answer:
The value of charge q is:
q=−Q4
- Charge +Q is at x = 0.
- Charge +Q is at x = d.
- Charge q is at x = d/2.
- The charge at x = d will exert a repulsive force on the charge at the origin (since both are positive).
- The charge at x = d/2 will also exert a force on the charge at the origin. The nature of this force will depend on the sign of charge q.
- If q is positive, it will repel the charge at the origin, adding to the force from the charge at x = d.
- If q is negative, it will attract the charge at the origin, opposing the repulsive force from the charge at x = d.
- The force due to the charge at x = d on the charge at x = 0 is given by:
F+Q=kQ⋅Qd2=kQ2d2
- The force due to the charge q at x = d/2 on the charge at x = 0 is given by:
Fq=kQ⋅q(d/2)2=k4Qqd2
- For the net force on the charge at x = 0 to be zero, the attractive force from charge q must balance the repulsive force from the charge at x = d:
k4Qqd2=kQ2d2
- We can cancel out k and d2 from both sides:
4Qq=Q2
- Rearranging gives:
q=Q24Q=Q4
- Since we assumed q must be negative for the forces to balance, we conclude:
q=−Q4
The value of charge q is:
q=−Q4
Similar Questions
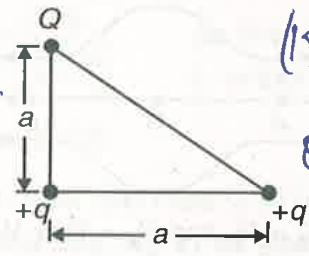
Three charges +q , +q, and Q are placed at the comers of a right angled isosceles triangle as shown in the figure. If the net potential energy of the system is zero then value of Q is
View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

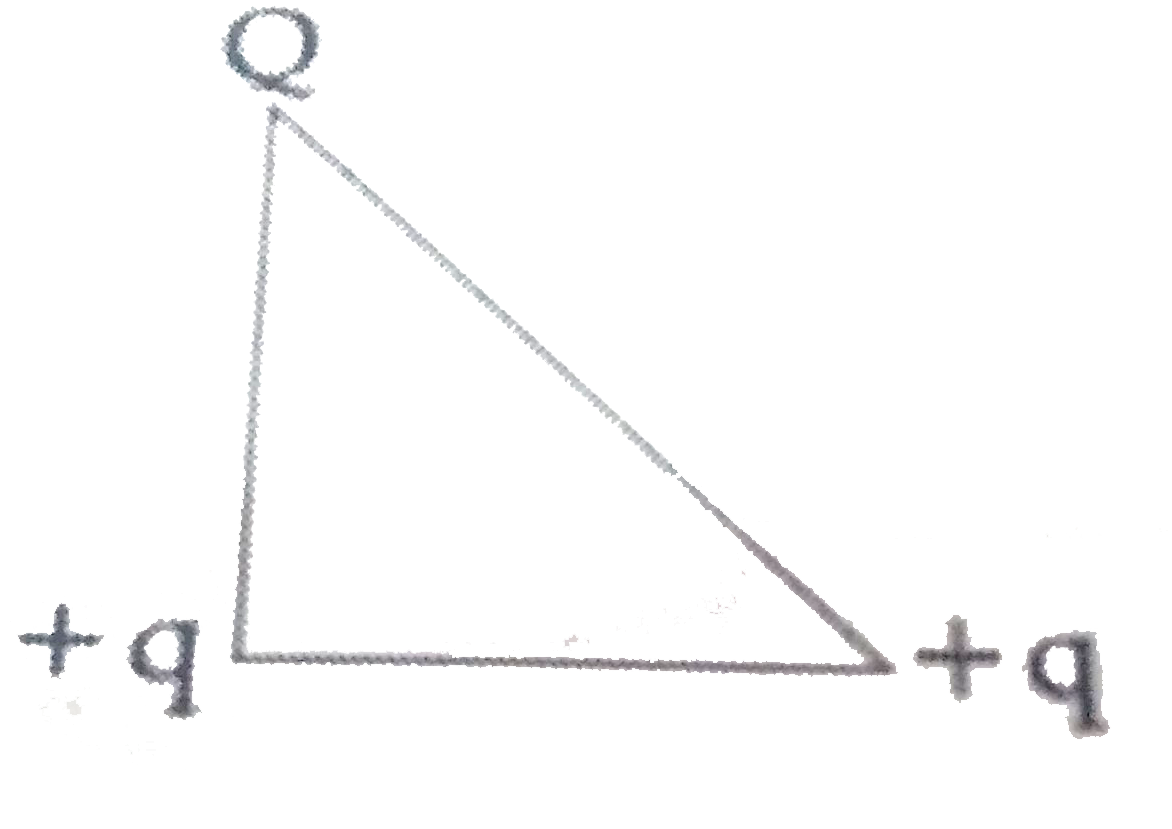
View SolutionThree charges Q+q and + q are placed at the vertices of a right -angle isosceles triangle as shown below. The net eletrostatic energy of the configuration is zero if the value of Q is :
View SolutionThe charges - q, Q, -q are placed along x-axis at x = 0, x = a and x = 2a. If the potential energy of the system is zero, then Q:q is
View SolutionThree charge q,Q and −4q are placed in a straight line , line of length Lat points distant 0,L/2 and L respectively from one end. In order to make the net force on q zero, the charge Q must be equal to
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionThree point charges Q1,Q2andQ3 in that order are placed equally spaced along a striaght line. Q2andQ3 are equal in magnitude but opposite is sign. If the net force on Q3 is zero, the value of Q1 is
View SolutionA positive point charge q is fixed at origin. A dipole with a dipole momen →p is placed along the x-axis for away from the orgin with →p poiniting along positive x-axis .
(i) If the kinetic energy of the diople when it reachers a distance d from the origin is qp4πε0dn, then n is .
(ii) If the force experienced by the charge q at this moment is 4qpπε0d3,ˆi then x is.
View SolutionTwo electric charges q1=qandq2=−2q are placed at a distance l = 6a apart. Find the locus of points in the plane of the charges where the field potential is zero
View Solution
