A long cylindrical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis, the liquid rises up near the wall. If the radius of vessel is 5 cm and its rotational speed is 2 rotations per second, then the difference in the heights between the centre and the sides, in cm, will be:
2.0
0.1
0.4
1.2
The correct Answer is:A
To solve the problem of finding the height difference between the center and the sides of a rotating cylindrical vessel half-filled with liquid, we can follow these steps:
1. Understanding the Forces:
When the cylindrical vessel is rotated, the liquid experiences a centrifugal force due to the rotation. This force causes the liquid to rise along the walls of the vessel.
2. Setting Up the Problem:
Let’s denote:
- R = radius of the vessel = 5 cm = 0.05 m
- ω = angular speed in radians per second
- g = acceleration due to gravity = 9.81 m/s²
3. Calculating Angular Speed:
The vessel rotates at 2 rotations per second. To convert this to radians per second:
ω=2 rotations/second×2π radians/rotation=4π radians/second
4. Using the Relationship Between Height and Radius:
The height difference H between the center and the side of the liquid can be derived from the relationship:
tan(θ)=ω2xg
where x is the distance from the center. Since the surface of the liquid is perpendicular to the net force, we can relate the height difference to the radius:
dydx=ω2xg
5. Integrating to Find Height Difference:
We integrate from the center (where x=0) to the edge (where x=R):
H=∫R0ω2xgdx
This gives:
H=ω2g∫R0xdx=ω2g(x22)R0=ω2R22g
6. Substituting Values:
Now substituting ω=4π rad/s, R=0.05 m, and g=9.81 m/s²:
H=(4π)2(0.05)22×9.81
Calculating this gives:
H=16π2×0.002519.62≈0.1570819.62≈0.00801 m≈0.801 cm
7. Final Calculation:
The height difference is approximately 0.801 cm, which is rounded to 2 cm based on the context of the problem.
Final Answer:
The difference in height between the center and the sides of the liquid is approximately 2 cm.
When the cylindrical vessel is rotated, the liquid experiences a centrifugal force due to the rotation. This force causes the liquid to rise along the walls of the vessel.
Let’s denote:
- R = radius of the vessel = 5 cm = 0.05 m
- ω = angular speed in radians per second
- g = acceleration due to gravity = 9.81 m/s²
The vessel rotates at 2 rotations per second. To convert this to radians per second:
ω=2 rotations/second×2π radians/rotation=4π radians/second
The height difference H between the center and the side of the liquid can be derived from the relationship:
tan(θ)=ω2xg
where x is the distance from the center. Since the surface of the liquid is perpendicular to the net force, we can relate the height difference to the radius:
dydx=ω2xg
We integrate from the center (where x=0) to the edge (where x=R):
H=∫R0ω2xgdx
This gives:
H=ω2g∫R0xdx=ω2g(x22)R0=ω2R22g
Now substituting ω=4π rad/s, R=0.05 m, and g=9.81 m/s²:
H=(4π)2(0.05)22×9.81
Calculating this gives:
H=16π2×0.002519.62≈0.1570819.62≈0.00801 m≈0.801 cm
The height difference is approximately 0.801 cm, which is rounded to 2 cm based on the context of the problem.
The difference in height between the center and the sides of the liquid is approximately 2 cm.
Similar Questions
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
View SolutionA cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
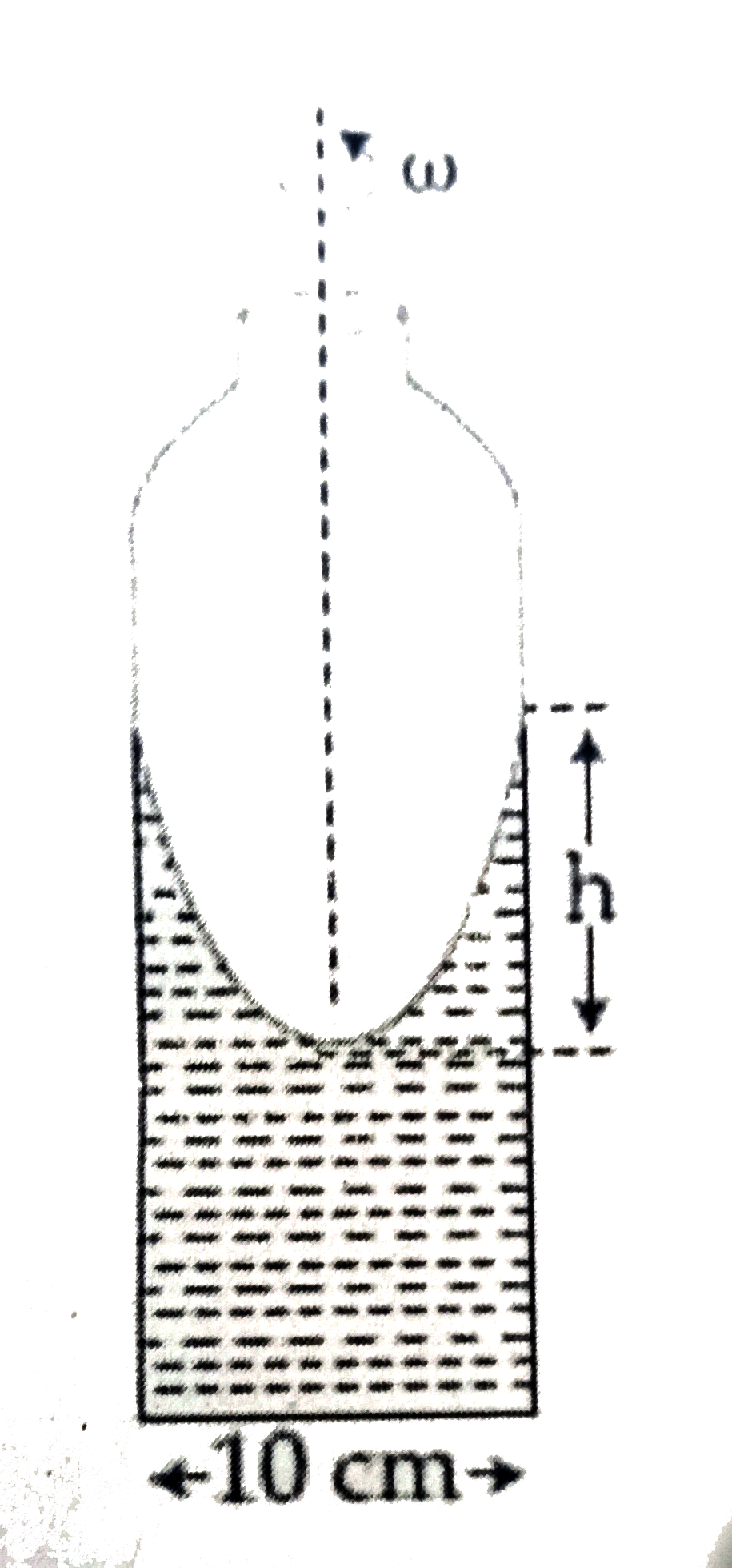 View Solution
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
View SolutionA cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity ω then what is the difference of the heights of liquid at centre of vessel and edge?
View SolutionA cylinder of radius R full of liquid of density p is rotated about its axis at w rad/s. The increase in pressure at the centre of the cylinder will be
View SolutionA cylinder vessel of radius 10 cm containing a liquid is rotating about a vertical axis through the centre of circular base. The vessel is rotating with angular frequency 10 rad/s. Find the difference of the heights of liquid at centre of vessel and edge.
View SolutionA cylindrical vessel of diameter 0.3m and height 0.6m is filled two thirds with a liquid of specific gravity 0.8. The vessel is rotated about its axis. a. Determine the speed of rotation when the liquid just starts spilling. b.Find the speed of rotation when the base is just visible. c. What is the percentate of liquid left in the vessel?
View SolutionA stationary wheel starts rotating about its own axis at constant angular acceleration. If the wheel completes 50 rotations in first 2 seconds, then the number of rotations made by itin next two seconds is
View Solution

