A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
0.001 m
0.002 m
0.01 m
0.02 m
The correct Answer is:D
To solve the problem, we need to find the difference in height of the liquid in a cylindrical vessel that is rotating around its axis. Here’s a step-by-step solution:
Step 1: Understand the parameters given
- Radius of the vessel, r=0.05m
- Speed of rotation, f=2rev/s
Step 2: Convert the speed of rotation to angular velocity
Angular velocity ω in radians per second can be calculated using the formula:
ω=2πf
Substituting the value of f:
ω=2π×2=4πrad/s
Step 3: Calculate the linear velocity v
The linear velocity v at the edge of the vessel is given by:
v=ωr
Substituting the values of ω and r:
v=4π×0.05=0.2πm/s
Step 4: Use the formula for height difference
The difference in height h of the liquid at the center and at the sides of the vessel is given by:
h=v22g
Where g is the acceleration due to gravity (approximately 10m/s2).
Step 5: Substitute v into the height difference formula
First, calculate v2:
v2=(0.2π)2=0.04π2m2/s2
Now, substitute v2 into the height difference formula:
h=0.04π22×10=0.04π220=0.002π2m
Step 6: Calculate the numerical value of h
Using π≈3.14:
h≈0.002×(3.14)2=0.002×9.8596≈0.0197m
This can be approximated to:
h≈0.02m
Conclusion
The difference in the height of the liquid at the center of the vessel and its sides is approximately 0.02m.
---
- Radius of the vessel, r=0.05m
- Speed of rotation, f=2rev/s
Angular velocity ω in radians per second can be calculated using the formula:
ω=2πf
Substituting the value of f:
ω=2π×2=4πrad/s
The linear velocity v at the edge of the vessel is given by:
v=ωr
Substituting the values of ω and r:
v=4π×0.05=0.2πm/s
The difference in height h of the liquid at the center and at the sides of the vessel is given by:
h=v22g
Where g is the acceleration due to gravity (approximately 10m/s2).
First, calculate v2:
v2=(0.2π)2=0.04π2m2/s2
Now, substitute v2 into the height difference formula:
h=0.04π22×10=0.04π220=0.002π2m
Using π≈3.14:
h≈0.002×(3.14)2=0.002×9.8596≈0.0197m
This can be approximated to:
h≈0.02m
The difference in the height of the liquid at the center of the vessel and its sides is approximately 0.02m.
Similar Questions
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
View SolutionA cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
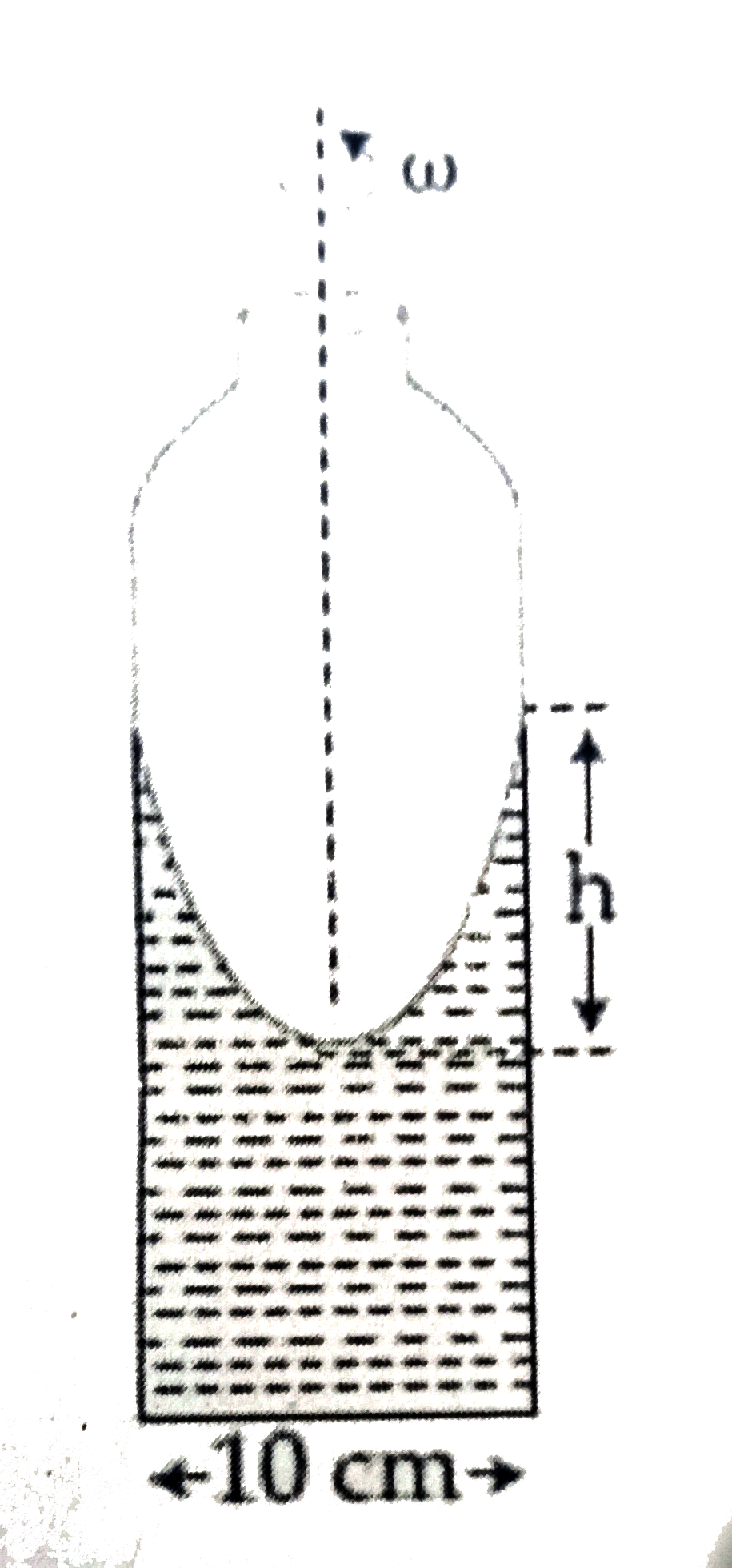 View Solution
View SolutionA long cylindrical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis, the liquid rises up near the wall. If the radius of vessel is 5 cm and its rotational speed is 2 rotations per second, then the difference in the heights between the centre and the sides, in cm, will be:
View SolutionA cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity ω then what is the difference of the heights of liquid at centre of vessel and edge?
View SolutionA cylinder vessel of radius 10 cm containing a liquid is rotating about a vertical axis through the centre of circular base. The vessel is rotating with angular frequency 10 rad/s. Find the difference of the heights of liquid at centre of vessel and edge.
View SolutionThe apparent depth of a liquid in a vessel is 15 cm, when its real depth is 20 cm. find the refractive index of the liquid.
View SolutionA fluid having a thermal coefficient of volume expansion γ is filled in a cylindrical vessel up to a height h0. The coefficient of linear thermal expansion of the material of the vessel is α . If the fluid is heated with the vessel , then find the level of liquid when temperature increases by Δθ.
View SolutionA cylindrical vessel, without lid, has to be tin-coated on its both sides. If the radius of the base is 70cm and its height is 1.4m, calculate the cost of tin-coating at the rate of Rs. 3.50 per 1000 cm2
View Solution

