A wire of length l = 3m and area of cross section 10−2cm2 and breaking stress 4.8×10−7Nm2 is attached with block of mass 10kg. Find the maximum possible value of angular velocity with which block can be moved in circle with string fixed at one end.
The correct Answer is:4 rad//sec
To find the maximum possible value of angular velocity with which a block can be moved in a circle using a wire, we need to consider the forces acting on the block and the properties of the wire.
1. Identify the Given Data:
- Length of the wire, l=3m
- Area of cross-section, A=10−2cm2=10−2×10−4m2=10−6m2
- Breaking stress, σ=4.8×10−7N/m2
- Mass of the block, m=10kg
2. Calculate the Breaking Force:
The breaking force Fb can be calculated using the formula:
Fb=σ×A
Substituting the values:
Fb=4.8×10−7N/m2×10−6m2=4.8×10−13N
3. Relate Breaking Force to Centripetal Force:
For circular motion, the centripetal force Fc required to keep the block moving in a circle is given by:
Fc=m⋅v2r
where v is the linear velocity and r is the radius of the circle (which is equal to the length of the wire, l).
Since v=r⋅ω (where ω is the angular velocity), we can rewrite the centripetal force as:
Fc=m⋅(l⋅ω)2l=m⋅l⋅ω2
4. Set Breaking Force Equal to Centripetal Force:
To find the maximum angular velocity before the wire breaks, set the breaking force equal to the centripetal force:
Fb=m⋅l⋅ω2
Substituting the values:
4.8×10−13=10⋅3⋅ω2
5. Solve for Angular Velocity ω:
Rearranging the equation gives:
ω2=4.8×10−1330
ω2=1.6×10−14
Taking the square root:
ω=√1.6×10−14≈1.26×10−7rad/s
Final Answer:
The maximum possible value of angular velocity ω with which the block can be moved in a circle is approximately:
ω≈1.26×10−7rad/s
- Length of the wire, l=3m
- Area of cross-section, A=10−2cm2=10−2×10−4m2=10−6m2
- Breaking stress, σ=4.8×10−7N/m2
- Mass of the block, m=10kg
The breaking force Fb can be calculated using the formula:
Fb=σ×A
Substituting the values:
Fb=4.8×10−7N/m2×10−6m2=4.8×10−13N
For circular motion, the centripetal force Fc required to keep the block moving in a circle is given by:
Fc=m⋅v2r
where v is the linear velocity and r is the radius of the circle (which is equal to the length of the wire, l).
Since v=r⋅ω (where ω is the angular velocity), we can rewrite the centripetal force as:
Fc=m⋅(l⋅ω)2l=m⋅l⋅ω2
To find the maximum angular velocity before the wire breaks, set the breaking force equal to the centripetal force:
Fb=m⋅l⋅ω2
Substituting the values:
4.8×10−13=10⋅3⋅ω2
Rearranging the equation gives:
ω2=4.8×10−1330
ω2=1.6×10−14
Taking the square root:
ω=√1.6×10−14≈1.26×10−7rad/s
The maximum possible value of angular velocity ω with which the block can be moved in a circle is approximately:
ω≈1.26×10−7rad/s
Topper's Solved these Questions
Similar Questions
A bob of mass 10 kg is attached to wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross section of the wire is 10−6m2. The maximum angular velocity with which it can be rotated in a horizontal circle
View SolutionA bob of mass 10 kg is attached to wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross section of the wire is 10−6m2. The maximum angular velocity with which it can be rotated in a horizontal circle
View SolutionA bob of mass 10kg is attached to a wire 0.3m long. Its breaking stress is 4.8×107N/m2. Then area of cross-section of the wire is 10−6m2. What is the maximum angular velocity with which it can be rotated in a horizontal circle?
View SolutionTwo block of mass m and M are connected means of a metal of a metal wire passing over a frictionless fixed pulley. The area of cross section of the wire is 6.67×10−9m2 and its breaking stress is 2×109Nm−2. If m = 1kg. Find the maximum value of M in kg for which the wire will not break. (g=10m/s2).
View SolutionThe breaking stress of steel is 7.85×108N/m2 and density of steel is 7.7×103kg/m3. The maximum frequency to which a string 1m long can be tuned is
View SolutionSpeed of transverse wave in a string of density 100kg/m3 and area of cross-section 10mm2 under a tension of 103 N is
View Solution
A steel wire of length 60 cm and area of cross section 10−6m2 is joined with a n aluminium wire of length 45 cm and are of cross section 3×10−6m2. The composite string is stretched by a tension of 80 N. Density of steel is 7800kgm−3 and that of aluminium is 2600kgm−3 the minimum frequency of tuning fork. Which can produce standing wave in it with node at joint is
View SolutionA mass of 20kg is attached to one end of a steel wire 50cm long and is rotated in a horizontal circle. The area of cross-section of the wrie is 10−6m2 and the breaking stress for it is 4.8×107Pa. Calculate the maximum velocity with which the mass can be rotated.
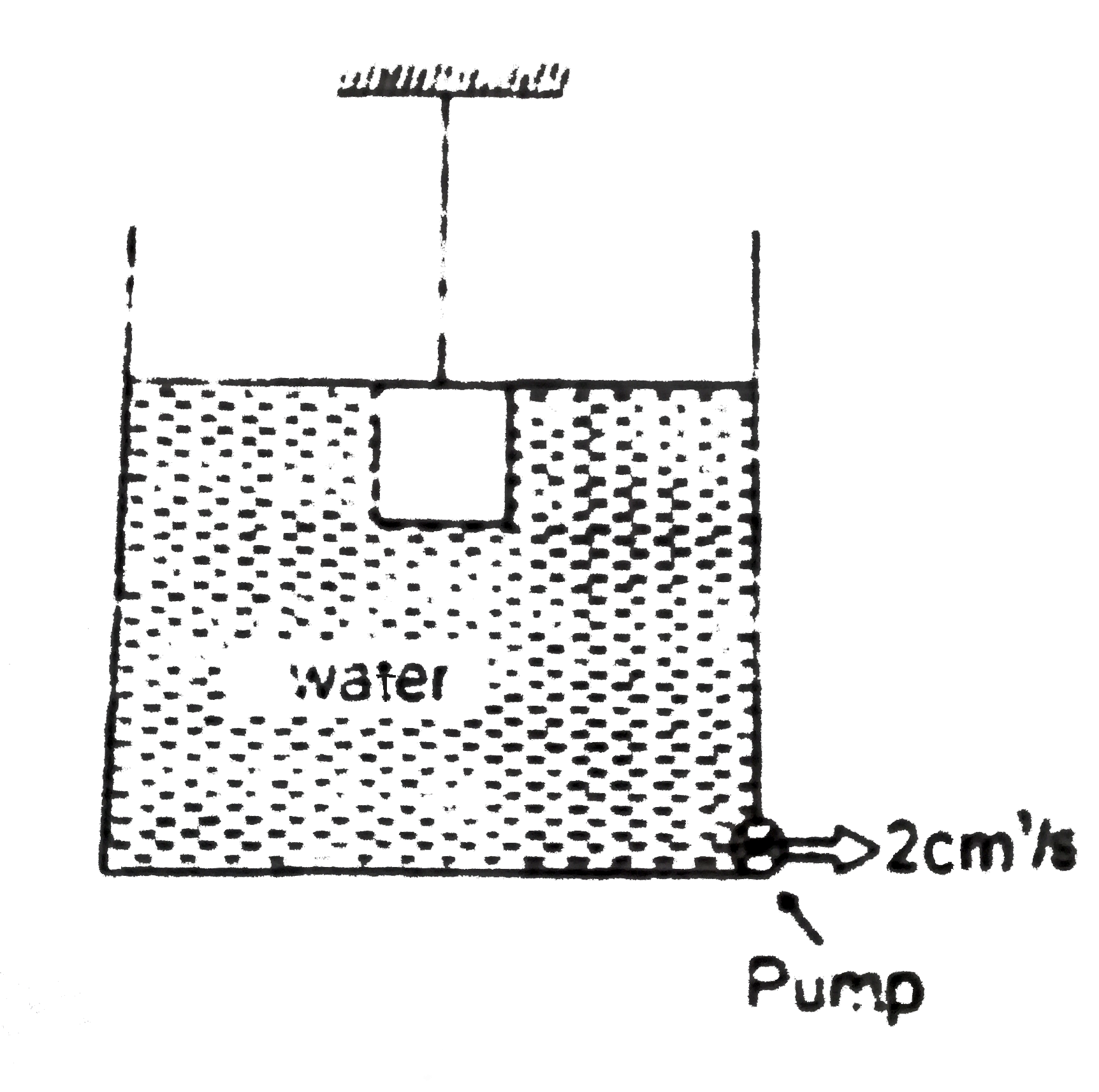
View SolutionFigure shows a cubical block of side 10 cm and relative density 1.5 suspended by a wire of cross sectional area 10−6m2. The breaking stress of the wire is 7×106N/m2. The block is placed in a beaker of base area 200cm2 and initially i.e. at t = 0, the top surface of water & the block coincide. There is a pump at the bottom corner which ejects 2cm3 of water per sec. Find the time at which the wire will break.
View SolutionTwo bodies of masses 2kg and 3kg are connected by a metel wire of cross section 0.04 mm2. Breaking stress of metel wire is 2.5 Gpa. The maximum force F that can be applied to 3kg block so that wire does not break is :

View Solution
