An ideal diatomic gas is taken through an adiabatic process in which density increases to 32 times. If pressure increases to 'n' times. Find n
4
8
64
128
The correct Answer is:D
To solve the problem, we need to analyze the adiabatic process of an ideal diatomic gas and how the changes in density affect the pressure. Here’s a step-by-step solution:
Step 1: Understand the relationship between density, mass, and volume
The density (ρ) of a gas is defined as:
ρ=mV
where m is the mass and V is the volume. Since the mass of the gas remains constant during the process, if the density increases to 32 times its initial value, we can express this as:
ρ′=32ρ
Step 2: Relate the change in density to the change in volume
From the definition of density, we can write:
ρ′=mV′andρ=mV
Thus, we have:
ρ′ρ=VV′=32
This implies:
V′V=132
Step 3: Use the adiabatic condition for an ideal gas
For an adiabatic process involving an ideal diatomic gas, the relationship between pressure (P), volume (V), and the adiabatic exponent (γ) is given by:
PVγ=constant
For a diatomic gas, the adiabatic exponent γ is:
γ=75
Step 4: Set up the equation for the initial and final states
Let P be the initial pressure and P′ be the final pressure. The relationship can be expressed as:
P′V′75=PV75
Dividing both sides by P:
P′P=(VV′)75
Step 5: Substitute the volume ratio
From Step 2, we know:
VV′=32
Substituting this into the equation gives:
P′P=3275
Step 6: Calculate 3275
We can express 32 as 25:
3275=(25)75=27
Thus:
P′P=27
Step 7: Find the value of n
From the equation above, we see that:
P′=27P
This means that the pressure increases by a factor of n=27=128.
Final Answer
Thus, the value of n is:
128
The density (ρ) of a gas is defined as:
ρ=mV
where m is the mass and V is the volume. Since the mass of the gas remains constant during the process, if the density increases to 32 times its initial value, we can express this as:
ρ′=32ρ
From the definition of density, we can write:
ρ′=mV′andρ=mV
Thus, we have:
ρ′ρ=VV′=32
This implies:
V′V=132
For an adiabatic process involving an ideal diatomic gas, the relationship between pressure (P), volume (V), and the adiabatic exponent (γ) is given by:
PVγ=constant
For a diatomic gas, the adiabatic exponent γ is:
γ=75
Let P be the initial pressure and P′ be the final pressure. The relationship can be expressed as:
P′V′75=PV75
Dividing both sides by P:
P′P=(VV′)75
From Step 2, we know:
VV′=32
Substituting this into the equation gives:
P′P=3275
We can express 32 as 25:
3275=(25)75=27
Thus:
P′P=27
From the equation above, we see that:
P′=27P
This means that the pressure increases by a factor of n=27=128.
Thus, the value of n is:
128
Topper's Solved these Questions
Similar Questions
Ideal gas is taken through the process shown in the figure :
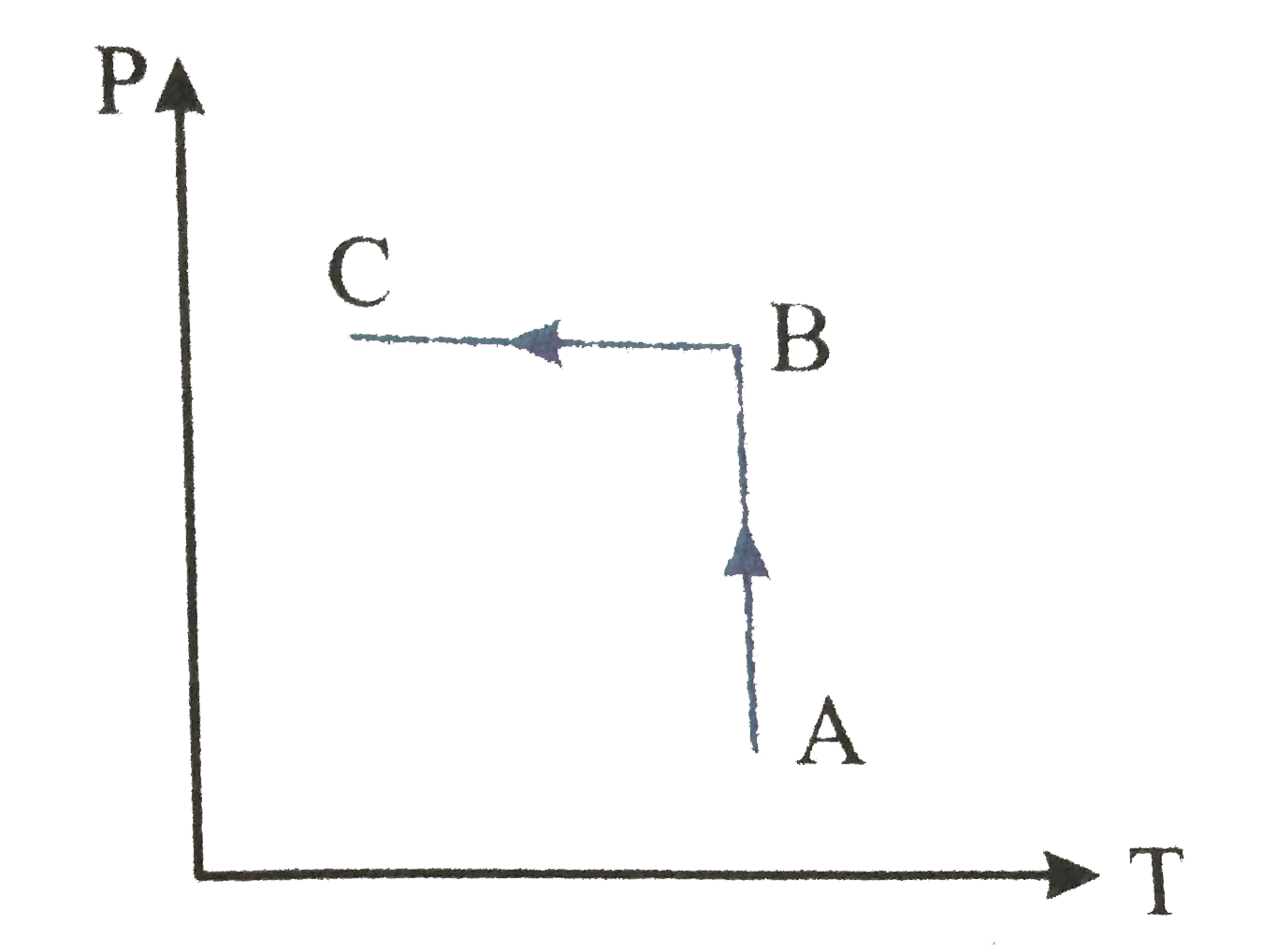
View SolutionIdeal gas is taken through the process shown in the figure :

View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
View SolutionTwo moles of an ideal diatomic gas is taken through a process VT2= constant so that its temperature increases by ΔT=300K. The ratio (ΔUΔQ) of increase in internal energy and heat supplied to the gas during the process is
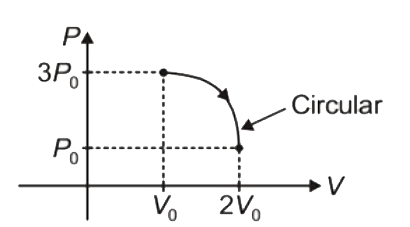
View SolutionOne mole of an ideal diatomic gas is taken through a process whose P−V diagram is shown in the figure. The work done by the gas is
View SolutionA diatomic gas expands adiabatically so that final density is 32 times the initial density. Find pressure becomes N times of initial presurre . the value of N is:
View SolutionOne litre of an ideal gas at a pressure of 6 atm undergoes an adiabatic expansion until its pressure drops to one atmosphere and volume increases to 2 litre. Find the word done during the process. [γ=1.4].
View SolutionAn ideal mono atomic gas is taken through the cyclic process shown in fig. Linear expansion from A to B following by adiabatic compression back to original state

View SolutionThe diffusion coefficient of an ideal gas is proportional to its mean free path and mean speed. The absolute temperature of an ideal gas is increased 4 times and its pressure is increased 2 times.As a result, the diffusion coefficient of this gas increases x times. The value of x is........
View Solution4 moles of an ideal monoatomic gas is heated isobarically so that its absolute temperature increases 2 times. Then the entropy increment of the gas in this process is
View Solution