A ball is dropped from height h. If falls on liquid surface. Its velocity does not change when its enters in liquid. Find height h in terms of r = radius of ball, σ = density of liquid, ρ = density of ball η = coefficient of viscosity and g = acceleration due to gravity :
2r4g(ρ−σ)281η2
2r4g(ρ−σ)250η2
2r4g(ρ−σ)225η2
2r4g(ρ−σ)290η2
The correct Answer is:A
To solve the problem, we need to find the height h from which a ball is dropped such that its velocity remains constant when it enters a liquid. The forces acting on the ball when it enters the liquid must balance out.
1. Identify the forces acting on the ball:
- The weight of the ball W=mg acts downward.
- The buoyant force FB acts upward, given by FB=σV, where V is the volume of the ball.
- The viscous force Fv also acts upward, given by Fv=6πηrv, where v is the velocity of the ball.
2. Set up the equation for forces:
When the ball enters the liquid and its velocity does not change, the net force acting on it must be zero:
mg−FB−Fv=0
3. Express the forces in terms of density and volume:
The volume V of the ball is given by:
V=43πr3
Thus, the buoyant force becomes:
FB=σ(43πr3)
4. Substituting the forces into the equation:
Substituting W, FB, and Fv into the force balance equation gives:
ρ(43πr3)g−σ(43πr3)−6πηrv=0
5. Simplifying the equation:
Factor out 43πr3:
43πr3(ρg−σ)−6πηrv=0
Rearranging gives:
ρg−σ=6ηv43r2
6. Solving for velocity v:
Rearranging the equation gives:
v=38r2(ρg−σ)/η
7. Using kinematic equations to relate height h and velocity v:
The velocity of the ball just before it hits the liquid can be calculated using the third equation of motion:
v2=u2+2gh
Since the initial velocity u=0:
v2=2gh
8. Equating the two expressions for v:
Setting the two expressions for v equal gives:
38r2(ρg−σ)η=√2gh
9. Squaring both sides:
(38r2(ρg−σ)η)2=2gh
10. Rearranging to find h:
h=9r4(ρg−σ)2128η2g
Final Result:
Thus, the height h in terms of r, σ, ρ, η, and g is:
h=9r4(ρ−σ)2128η2g
- The weight of the ball W=mg acts downward.
- The buoyant force FB acts upward, given by FB=σV, where V is the volume of the ball.
- The viscous force Fv also acts upward, given by Fv=6πηrv, where v is the velocity of the ball.
When the ball enters the liquid and its velocity does not change, the net force acting on it must be zero:
mg−FB−Fv=0
The volume V of the ball is given by:
V=43πr3
Thus, the buoyant force becomes:
FB=σ(43πr3)
Substituting W, FB, and Fv into the force balance equation gives:
ρ(43πr3)g−σ(43πr3)−6πηrv=0
Factor out 43πr3:
43πr3(ρg−σ)−6πηrv=0
Rearranging gives:
ρg−σ=6ηv43r2
Rearranging the equation gives:
v=38r2(ρg−σ)/η
The velocity of the ball just before it hits the liquid can be calculated using the third equation of motion:
v2=u2+2gh
Since the initial velocity u=0:
v2=2gh
Setting the two expressions for v equal gives:
38r2(ρg−σ)η=√2gh
(38r2(ρg−σ)η)2=2gh
h=9r4(ρg−σ)2128η2g
Thus, the height h in terms of r, σ, ρ, η, and g is:
h=9r4(ρ−σ)2128η2g
Topper's Solved these Questions
Similar Questions
A ball is dropped from a height h above ground. Neglect the air resistance, its velocity (v) varies with its height (y) above the ground as :-
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View Solution
Knowledge Check
A ball is dropped from a height h on the ground If the coefficient of restitution is e, the height to which the ball goes up after it rebounds for the nth time is
Ahe2nBhenCe2nhDhe2n
A small ball is dropped from a certain height on the surface of a non-viscous liquid of density less than the density of ball. The motion of the ball is
View SolutionA ball of density ρ is dropped from a height on the surface of a non-viscous liquid of density 2ρ. Choose the correct options.

View SolutionAssertion: A ball is dropped from a certain height above the free suface of and ideal fluid. When the ball enters the liquid it mau accelerate or retard.
Reason: Ball accelerates of retards it all depends on the dinsity of ball and the density of liquid.

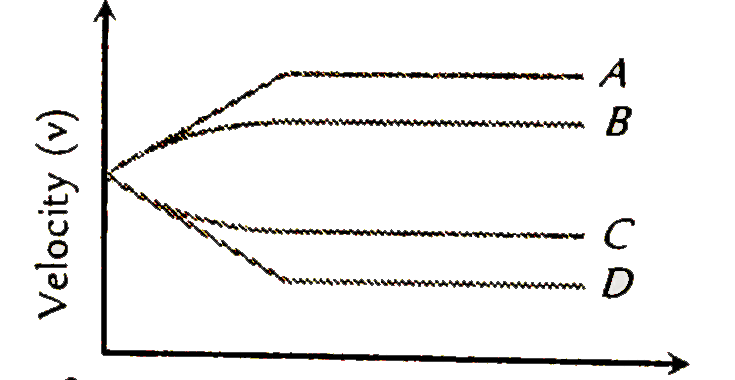
View SolutionA small spherical solid ball is dropped from a great height in a viscous liquid. Its journey in the liquid is best described in the diagram given below by the
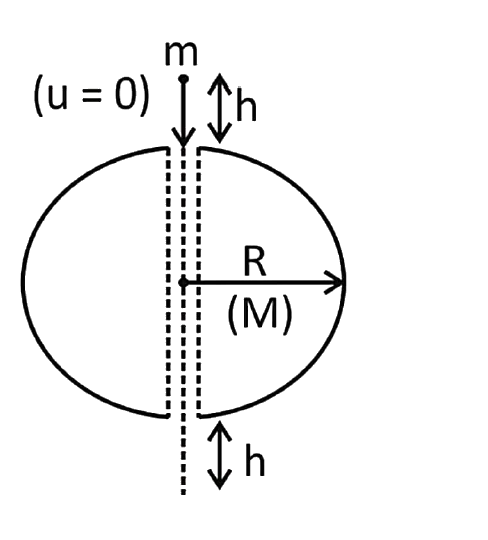
View SolutionA ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
View Solution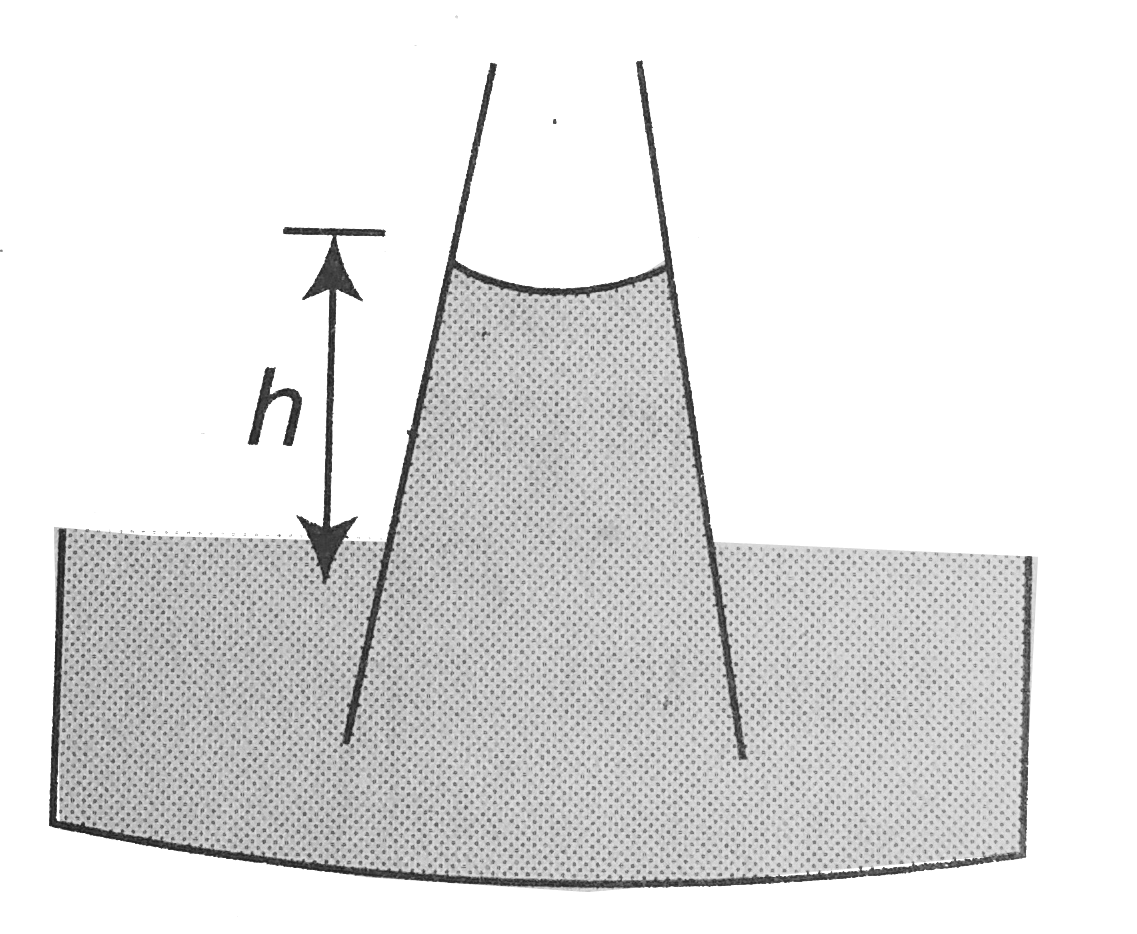
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View SolutionA ball of density ρ is released from deep inside of a liquid of density 2ρ. It will move up
View Solution
