A disc with moment of inertial I is rotating with some angular speed. Second disc is initially at rest. Now second disc with moment of inertia 3I is placed on first disc and starts rotating. Find loss of kinetic energy in fraction
56
14
0
34
To solve the problem, we will follow these steps:
Step 1: Understand the System
We have two discs:
- Disc 1 has a moment of inertia I and is rotating with an angular speed ω.
- Disc 2 has a moment of inertia 3I and is initially at rest.
Step 2: Apply Conservation of Angular Momentum
Since there are no external torques acting on the system, we can use the conservation of angular momentum. The initial angular momentum of the system is the angular momentum of Disc 1, as Disc 2 is at rest.
- Initial angular momentum Li:
Li=I⋅ω
After Disc 2 is placed on Disc 1, both discs rotate together with a common angular velocity ω1. The total moment of inertia of the system after placing Disc 2 is:
I+3I=4I
- Final angular momentum Lf:
Lf=(4I)⋅ω1
Setting initial and final angular momentum equal gives:
I⋅ω=4I⋅ω1
Step 3: Solve for ω1
Dividing both sides by I (assuming I≠0):
ω=4⋅ω1
Thus, we can express ω1 in terms of ω:
ω1=ω4
Step 4: Calculate Initial and Final Kinetic Energies
- Initial kinetic energy KEi (only Disc 1):
KEi=12Iω2
- Final kinetic energy KEf (both discs):
KEf=12(4I)ω21
Substituting ω1=ω4:
KEf=12(4I)(ω4)2=12(4I)⋅ω216=12I⋅ω24=18Iω2
Step 5: Calculate Loss of Kinetic Energy
The loss in kinetic energy ΔKE is given by:
ΔKE=KEi−KEf
Substituting the values:
ΔKE=12Iω2−18Iω2=(48−18)Iω2=38Iω2
Step 6: Calculate the Fraction of Loss in Kinetic Energy
The fraction of loss in kinetic energy is given by:
Fraction=ΔKEKEi=38Iω212Iω2
Cancelling Iω2 from the numerator and denominator:
Fraction=3/81/2=38⋅21=34
Conclusion
The loss of kinetic energy in fraction is 34.
We have two discs:
- Disc 1 has a moment of inertia I and is rotating with an angular speed ω.
- Disc 2 has a moment of inertia 3I and is initially at rest.
Since there are no external torques acting on the system, we can use the conservation of angular momentum. The initial angular momentum of the system is the angular momentum of Disc 1, as Disc 2 is at rest.
Li=I⋅ω
I+3I=4I
- Final angular momentum Lf:
Lf=(4I)⋅ω1
I⋅ω=4I⋅ω1
Dividing both sides by I (assuming I≠0):
ω=4⋅ω1
Thus, we can express ω1 in terms of ω:
ω1=ω4
- Initial kinetic energy KEi (only Disc 1):
KEi=12Iω2
KEf=12(4I)ω21
Substituting ω1=ω4:
KEf=12(4I)(ω4)2=12(4I)⋅ω216=12I⋅ω24=18Iω2
The loss in kinetic energy ΔKE is given by:
ΔKE=KEi−KEf
Substituting the values:
ΔKE=12Iω2−18Iω2=(48−18)Iω2=38Iω2
The fraction of loss in kinetic energy is given by:
Fraction=ΔKEKEi=38Iω212Iω2
Cancelling Iω2 from the numerator and denominator:
Fraction=3/81/2=38⋅21=34
The loss of kinetic energy in fraction is 34.
Topper's Solved these Questions
Similar Questions
A disc is rotating with angular speed ω1. The combined moment of inertia of the disc and its axle is I1. A second disc of moment of inertia I2 is dropped on to the first and ends up rotating with it. Find the angular velocity of the combination if the original angular velocity of the upper disc was (a) zero (b) ω2 in the same direction as ω1 and (c) ω2 in a direction opposite to ω1.
View SolutionA body is rotating with angular momentum L. If I is its moment of inertia about the axis of rotation is I, its kinetic energy of rotation is
View SolutionA circular disc of moment of inertia It is rotating in a horizontal plane about its symmetry axis with a constant angular velocity ωi. Another disc of moment of inertia Ib is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed ωf. Calculate the energy lost by the initially rotating disc due to friction.
View SolutionIf a disc of moment of inertia I and radius r is reshaped into a ring of radius nr, keeping its mass same, its moment of inertia becomes
View SolutionTwo uniform circular rough disc of moment of inertia I1 and I12 are rotating with angular velocity ω1 and ω12 respectively in same direction. Now one disc is placed the other disc co-axially. The change in kinetic energy of the system is :
View SolutionA uniform disc of moment of inertia 1kgm2 rotates with a speed of 120 rpm, Calculate the torque required to stop the disc in 10 revolutions ?
View SolutionMoment of inertia of a disc about an axis which is tangent and parallel to its plane is I . Then the moment of inertia of disc about a tangent, but perpendicular to its plane will be
View SolutionThe two uniform discs rotate separately on parallel axles. The upper disc (radius a and momentum of inertia I1) is given an angular velocity ω0 and the lower disc of (radius b and momentum of inertia I2) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is.
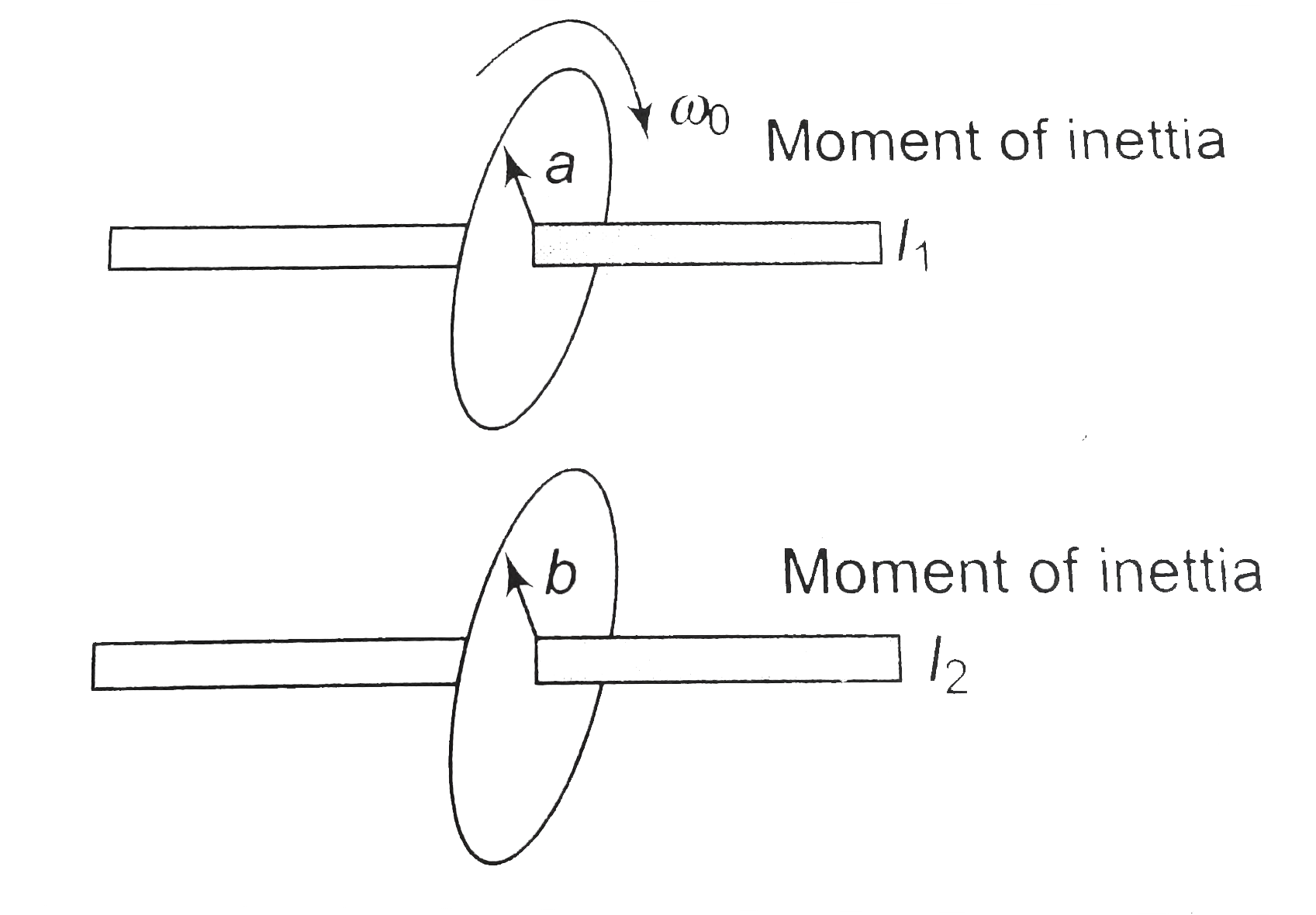 .
.
View SolutionIn the above question, angular displacement of the disc, in first two second will be in radian:
View SolutionTwo discs, each having moment of inertia 5kgm2. about its central axis, rotating with speeds 10rads−1 and 20rads−1, are brought in contact face to face with their axes of rotation coincided. The loss of kinetic energy in the process is
View Solution
