A square loop of side 2a and carrying current I is kept in xz plane with its centre at origin. A long wire carrying the same cruurent I is placed parallel to z - axis and passing through point (0,b,0), (b >>a). The magnitude of troque on the loop about z - axis will be :
μ0I2a22πb
μ0I2a32πb2
2μ0I2a2πb
2μ0I2a3πb2
To solve the problem of finding the torque on a square loop of side 2a carrying current I, placed in the xz-plane with its center at the origin, due to a long wire carrying the same current I parallel to the z-axis at point (0, b, 0), we will proceed step by step.
Step 1: Determine the Area of the Loop
The area A of the square loop can be calculated using the formula:
A=side2=(2a)2=4a2
Hint: Remember that the area of a square is given by the square of the length of one side.
Step 2: Find the Magnetic Moment
The magnetic moment →m of the loop is given by:
→m=I⋅→A
where →A is the area vector. The direction of the area vector can be determined using the right-hand rule. Since the current flows in a counterclockwise direction when viewed from the positive y-axis, the area vector points in the positive y-direction:
→A=4a2^j
Thus, the magnetic moment becomes:
→m=I⋅(4a2^j)=4a2I^j
Hint: The area vector points in the direction given by the right-hand rule based on the current's direction.
Step 3: Calculate the Magnetic Field Due to the Wire
The magnetic field →B at a distance b from a long straight wire carrying current I is given by:
B=μ0I2πb
The direction of the magnetic field due to the wire (using the right-hand rule) will be in the positive x-direction:
→B=μ0I2πb^i
Hint: Use the right-hand rule to determine the direction of the magnetic field around a current-carrying wire.
Step 4: Calculate the Torque on the Loop
The torque →τ on the loop is given by the cross product of the magnetic moment and the magnetic field:
→τ=→m×→B
Substituting the values we found:
→τ=(4a2I^j)×(μ0I2πb^i)
Calculating the cross product:
→τ=4a2I⋅μ0I2πb(^j×^i)=4a2I⋅μ0I2πb(−^k)
Thus, the magnitude of the torque is:
|→τ|=4a2⋅μ0I22πb=2μ0I2a2πb
Hint: The magnitude of the torque can be found by taking the magnitude of the cross product.
Final Answer
The magnitude of the torque on the loop about the z-axis is:
2μ0I2a2πb
The area A of the square loop can be calculated using the formula:
A=side2=(2a)2=4a2
The magnetic moment →m of the loop is given by:
→m=I⋅→A
where →A is the area vector. The direction of the area vector can be determined using the right-hand rule. Since the current flows in a counterclockwise direction when viewed from the positive y-axis, the area vector points in the positive y-direction:
→A=4a2^j
Thus, the magnetic moment becomes:
→m=I⋅(4a2^j)=4a2I^j
The magnetic field →B at a distance b from a long straight wire carrying current I is given by:
B=μ0I2πb
The direction of the magnetic field due to the wire (using the right-hand rule) will be in the positive x-direction:
→B=μ0I2πb^i
The torque →τ on the loop is given by the cross product of the magnetic moment and the magnetic field:
→τ=→m×→B
Substituting the values we found:
→τ=(4a2I^j)×(μ0I2πb^i)
Calculating the cross product:
→τ=4a2I⋅μ0I2πb(^j×^i)=4a2I⋅μ0I2πb(−^k)
Thus, the magnitude of the torque is:
|→τ|=4a2⋅μ0I22πb=2μ0I2a2πb
The magnitude of the torque on the loop about the z-axis is:
2μ0I2a2πb
Topper's Solved these Questions
Similar Questions
A square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA square loop ABCD , carrying a current I, is placed near and coplanar with a long straight conductor XY carrying a current I.

View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA square coil ABCD lying in x−y plane with its centre at origin. A long straight wire passing through origin carries a current i=2t in negative z-direction. The induced current in the coil is

View SolutionA square coil ABCD lying in x−y plane with its centre at origin. A long straight wire passing through origin carries a current i=2t in negative z-direction. The induced current in the coil is

View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.

View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.

View SolutionA rigid square loop of side 'a' and carrying current I2 is lying on a horizontal surface near a long current I1 carrying wire in the same plane as shown in figure. The net force on the loop to the wire will be :
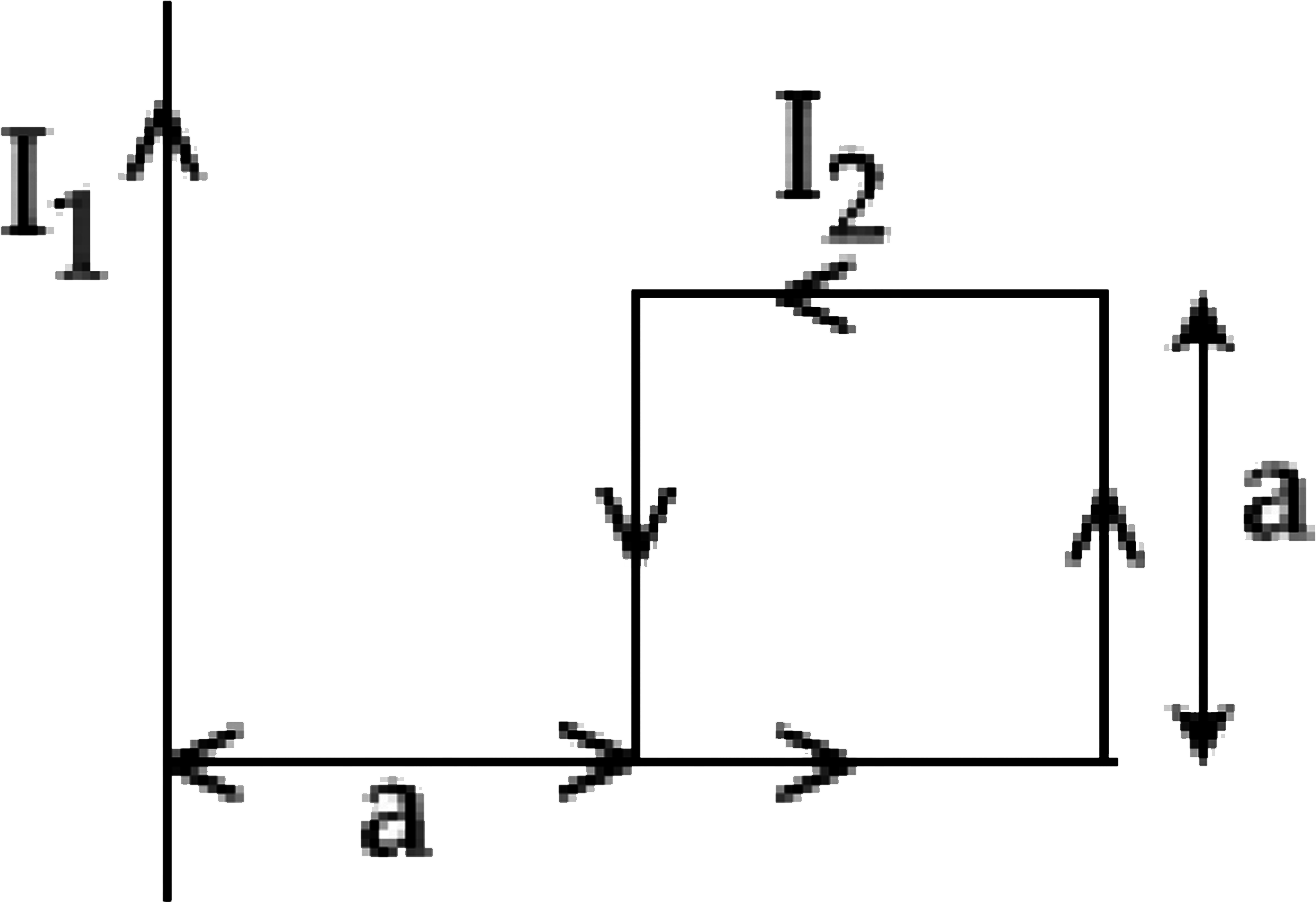
View SolutionA circular loop of radius R carrying current I is kept in XZ plane. A uniform and constant magnetic field →B=(B0ˆi+2B0ˆj+3B0ˆk) exists in the region (B0− a positive constant). Then the magnitude of the torque acting on the loop will be
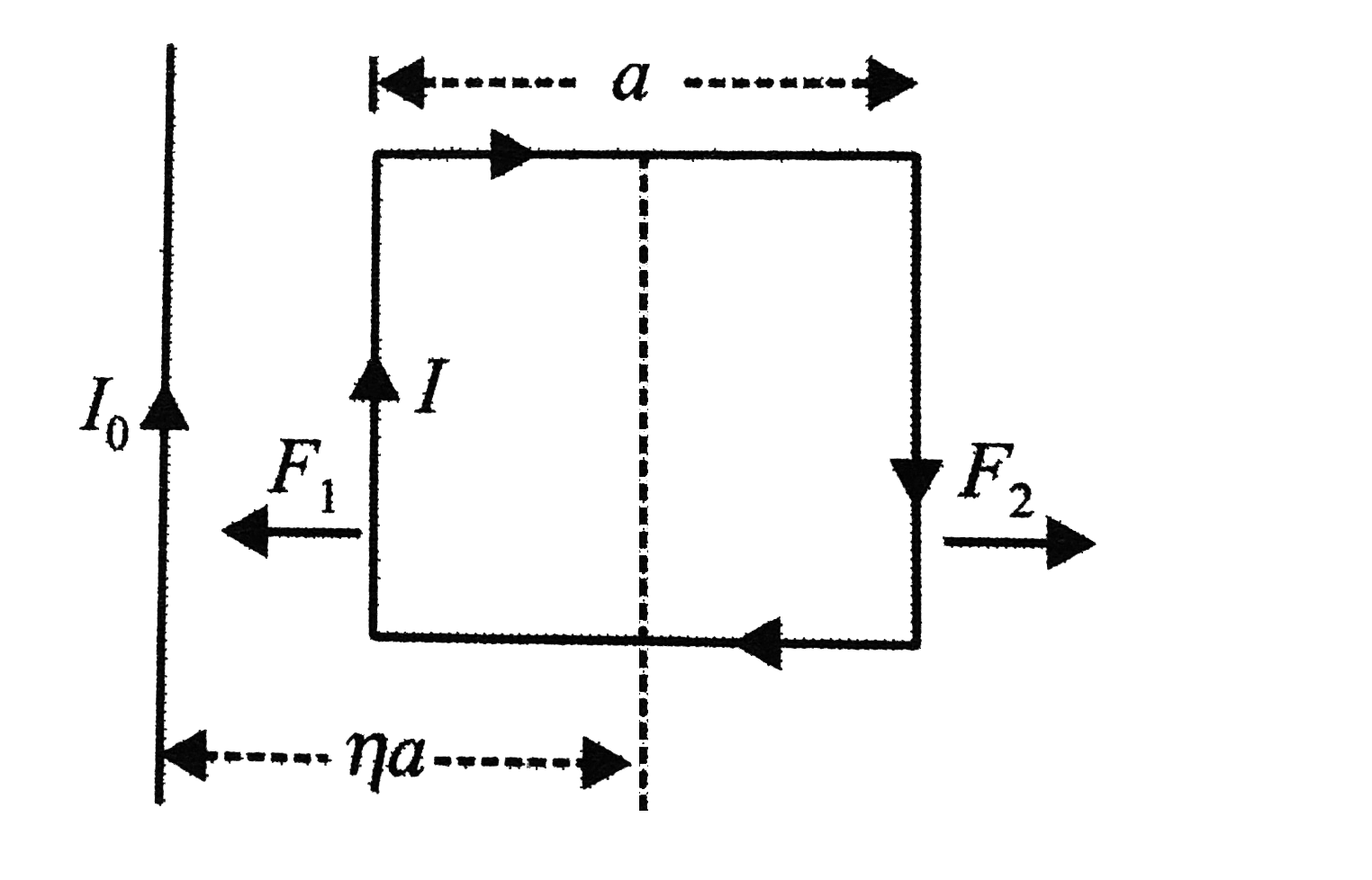
View SolutionA square frame carrying a current I=0.90A is located in the same plane as a long straight wire carrying a current I0=5A, The frame side has a length a=8cm. The axis of the frame passing through the mid-point of the opposite sides is parrallel to the wire and is separated form it by a distance h=15 times greater tahn the side of the frame.
Find:
(a) ampere force acting on the frame.
(b) The machanical work to be performed in order to turn the frmae through 180∘ about its axis, with the current maintained constant.
View Solution
