The pulley A and C are fixed while the pulley B is movable. A mass M2 is attached to pulley B , while the string has masses M1andM3 at the two ends. Find the acceleration of each mass .
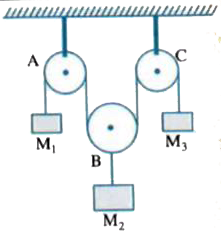
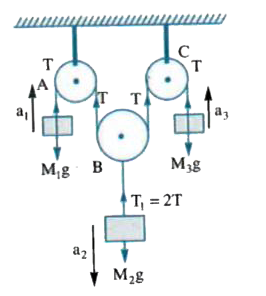
The force acting on masses M1,M2andM3 are shown in figure .
Let a2anda3 be upward acceleration of masses M1andM3anda2 the downward acceleration of mass M2 .
For motion of mass M1
T−M1g=M1a1....... (1)
For motion of mass M3
T−M3g=M3a3 ........ (2)
For motion of mass M2
M2g−2T=M2a2 ......... (3)
Let l1,l2,l3 be the lengths of vertical portions of the string between pulley at any instant. M1 goes up through x,M2 goes down through y and M3 goes up through z.
Then l1+2l2+l3=(l1−x)+2(l2+y)+l3−z
⇒x+z=2y⇒d2xdt2+d2zdt2=2d2ydt2
a1+a3=2a2⇒a2=a1+a32.......... (4)
From (1) , a1=TM1−g ....... (5)
From (2) ,a3=TM3−g ............ (6)
substituting a1anda3 is (4) , we get
a2=T2(1M1+1M3)−g......... (7)
From (3) , T=M2(g−a2)2 .......... (8)
substituting this value in (7) , we get
a2=M24(g−a2)(1M1+1M3)−gora2=M2(g−a2)(M3+M1)4M1M3−g
or4M1M3a2_M2(M1+M3)g−M2(M1+M3)a2−4M1M3g
or[4M1M3+M2(M1+M3)]a2=(M1+M3)M2g−4M1M3g
a2=(M1+M3)M2g−4M1M3g4M1M3+M2(M1+M3) a2=M1M2+M2M3−4M1M3M1M2+M2M3+4M1M3g...... (9)
substituting value of T from (8) in (5)
a1=M2(g−a2)2M1−g
Substituting value of a2 in above equation , we get
a1=−M1M−2+3M2M3−4M1M3M1M2+M2M3+4M1M3g ........ (10)
Similarly from (6) and (9)
a3=3M1M2−M2M3−4M1M3M1M2+M2M3−4M1M3 ........ (11)
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - LONG ANSWER TYPE QUESTIONS2videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - SHORT ANSWER TYPE QUESTION2videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - KINETIC THEORY OF GASESEXERCISE - Practice Exercise15videos
KINETIC THEORY OF GASES
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-343videos
MECHANICAL PROPERTIES OF FLUIDS
Similar Questions
Two block of masses m=5kgandM=10kg are connected by a string passing over a pulley B as shown. Another string connect the center of pulley B to the floor and passes over another pulley A as shown. An upwards force F is applied at the center of pulley A. Both the pulleys are massless.
Find the acceleration of block m and M, if F is
(a) 100N
(b)300N
(c)500N(Takeg=10m/s2)
 View Solution
View SolutionIf the string & all the pulleys are ideal, acceleration of mass m is :-
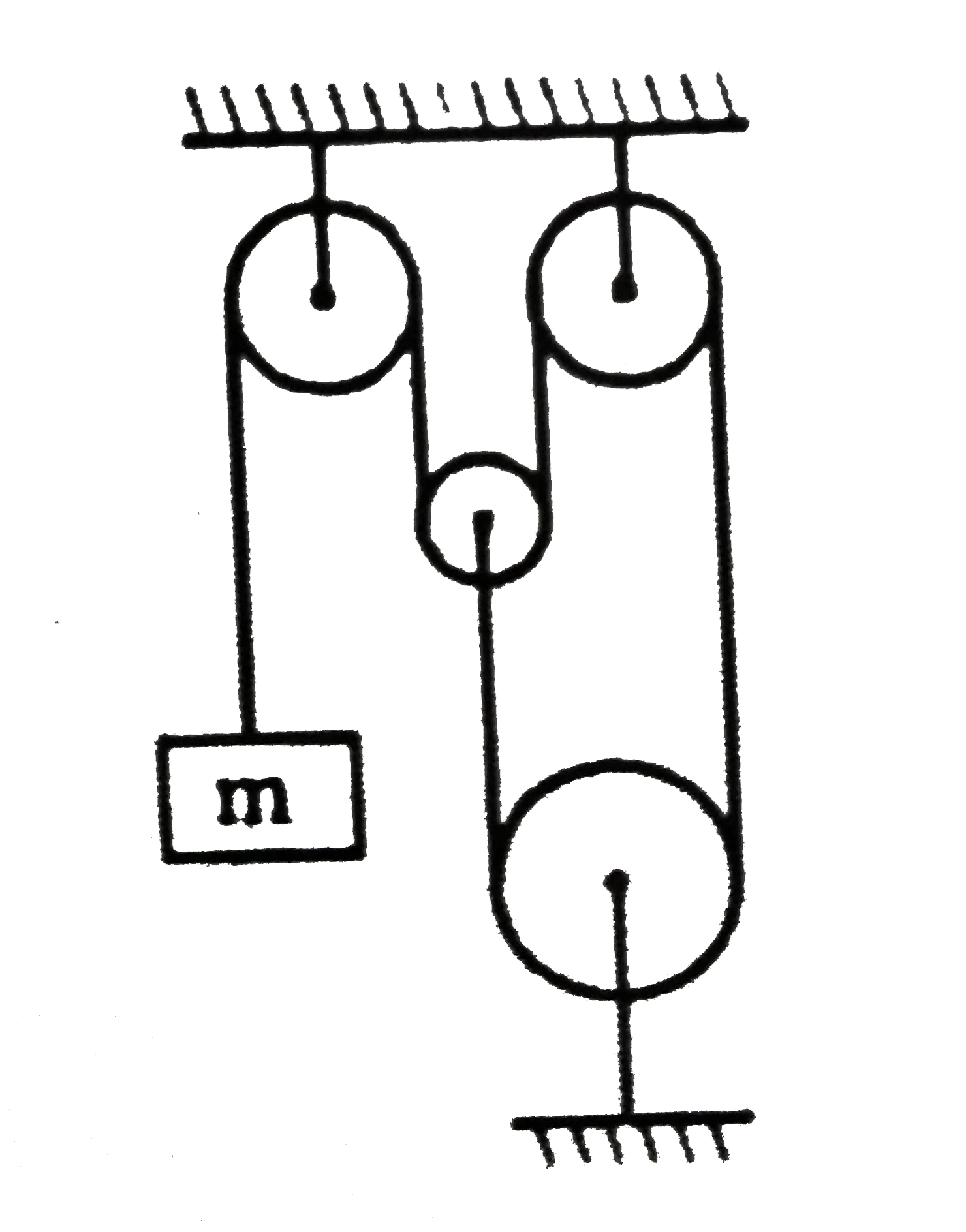 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
A7g8,g8B21g8,g8C21g8,g5D12g5,g5 - Question 2 - Select One
If the string & all the pulleys are ideal, acceleration of mass m is :-
 Ag2B0CgDdependent on m
Ag2B0CgDdependent on m
In the system shown in the figure all surfaces are smooth, pulley and string are massless. The string between the two pulleys and between pulley and block of mass 5 m is parallel to the incline surface of the block of mass 4 m. The system is released from rest. Find the acceleration of the block of mass 4 m . [tan37∘=34]
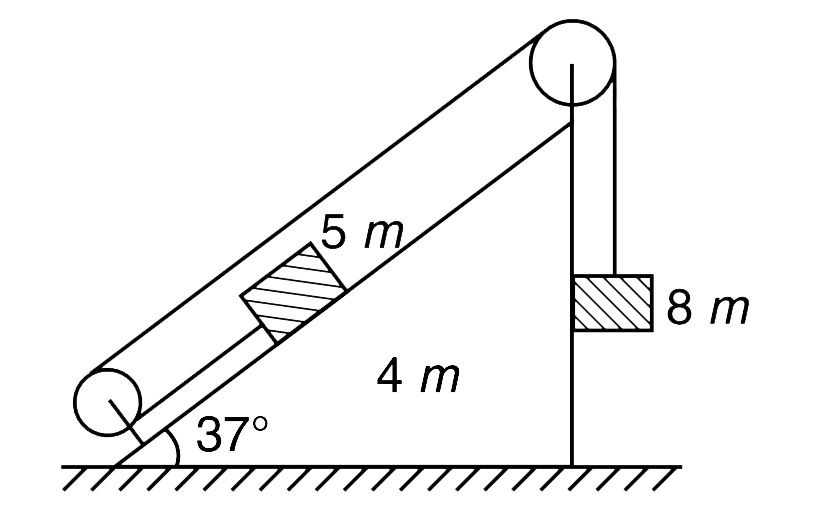 View Solution
View SolutionFigure shows two blocks of mass m and m connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley (uniform disc) has mass m and it can freely rotate about this axis. Find the acceleration of the mass m assuming that the string does not slip on the pulley.
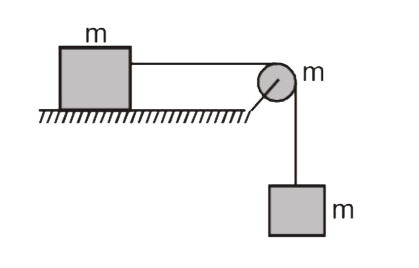 View Solution
View SolutionIn the pulley system shown the movable pulleys A,B and C have mass m each, D and E are fixed pulleys. The strings are vertical light and inextensible Then
 .View Solution
.View SolutionA smooth pulley A of mass M0 is lying on a frictionless table. A massless rope passes round the pulley and has masses M1 and M2 tied to its ends, the two portions of the string being perpendicular to the edge of the table so that the masses hang vertically. Find the acceleration of the pulley.
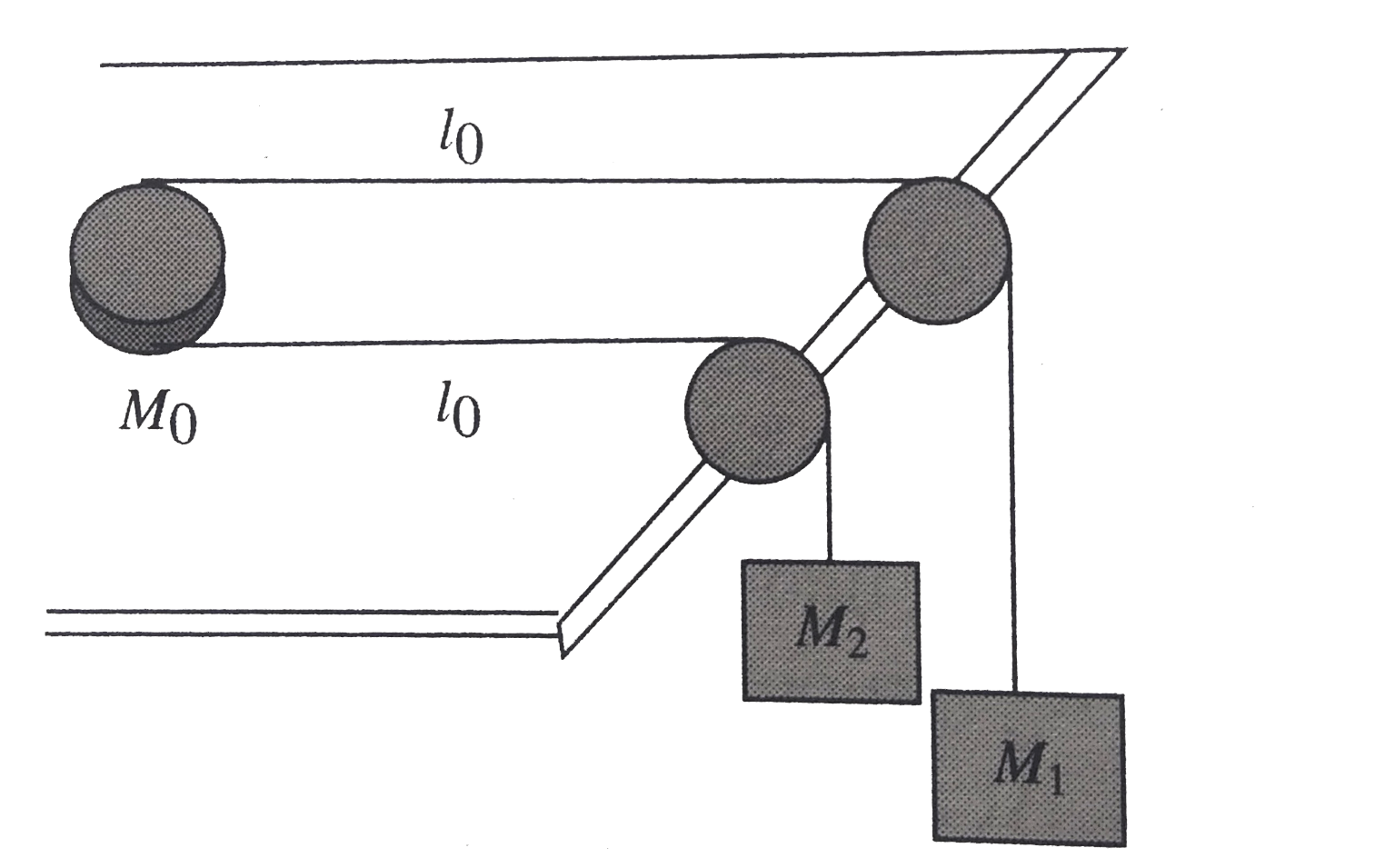 View Solution
View SolutionA smooth pulley A of mass M0 is lying on a frictionless table. A massless rope passes round the pulley and has masses M1 and M2 tied to its ends, the two portions of the string being perpendicular to the edge of the table so that the masses hang vertically. Find the acceleration of the pulley.
 View Solution
View SolutionString is wrapped over a pulley and free end is fixed to the ceiling as shown in figure. Mass of the pulley is m and its radius is R. Assume that pulley is identical to dise. Calculate acceleration of pulley as it is allowed to fall by unwinding the string. Assume that string does not slip over the pulley.
 View Solution
View Solution

