In tha above problem ,minimum value of t for which the intensity at point P on the screen exactly in fromt of the upper slit becomes maximum
0.167 s
0.5 s
0.012 s
0.3 s
The correct Answer is:A
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II ) LECTURE SHEET (ADVANCED ) (More Than one correct Type Questions)
4 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II ) LECTURE SHEET (ADVANCED ) (Linked Comprehension Type Questions)
3 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - I ) (MAIN) (Straight Objective Type Questions)
17 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
81 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
In the above problem, minimum value of t for which the intensity at point P on the screen exactly in front of the upper slit becomes maximum.
View SolutionIn young's double-slit experiment set up, sources S of wavelength 50 nm illumiantes two slits S1 and S2 which act as two coherent sources. The sources S oscillates about its own position according to the equation y=0.5sinπt, where y is in nm and t in seconds. The minimum value of time t for which the intensity at point P on the screen exaclty in front of the upper slit becomes minimum is
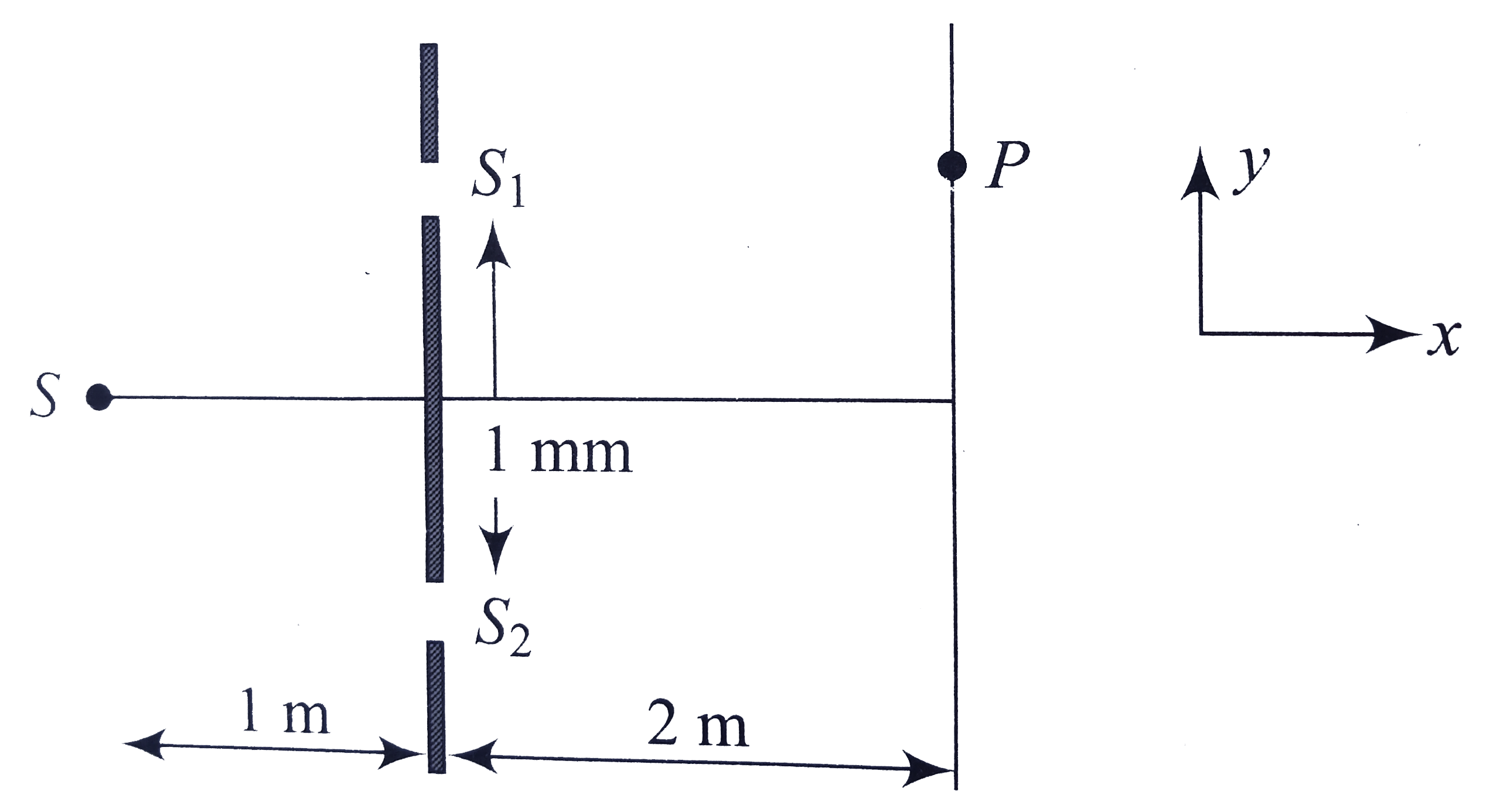
View Solution
Knowledge Check
In young's double-slit experiment set up, sources S of wavelength 50 nm illumiantes two slits S1 and S2 which act as two coherent sources. The sources S oscillates about its own position according to the equation y=0.5sinπt, where y is in nm and t in seconds. The minimum value of time t for which the intensity at point P on the screen exaclty in front of the upper slit becomes minimum is
 A1 sB2 sC3 sD1.5 s
A1 sB2 sC3 sD1.5 sIn a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen.
Find the value of n.A4B6C2D8In a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen. ltbr> Find the wavelength of light if the separation of slits is 2 mm.
A2.9×10−7mB3.9×10−7mC5.9×10−7mD6.9×10−7m
In a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen.
Find the value of n.
View SolutionIn a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen. ltbr> Find the wavelength of light if the separation of slits is 2 mm.
View SolutionIn young's double-slit experiment, both the slits produce equal intensities on a screen. A 100% transparent thin film of refractive index μ=1.5 is kept in front of one of the slits, due to which the intensity at the point O on the screen becomes 75% of its initial value. If the wavelength of monochromatic light is 720 nm, then what is the minimum thickness (in nm) of the film?
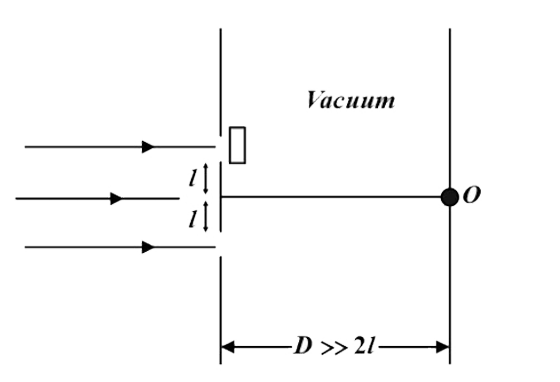
View SolutionIn young's double slit experiment relative intensity at a point on the screen may be defined as ratio of intensity at that point to the maximum intensity on the screen. Light of wavelength 7500∘A A passing through a double slit, produces interference pattern of relative intensity variation as shown in Fig. θ on horizontal axis represents the angular position of a point on the screen
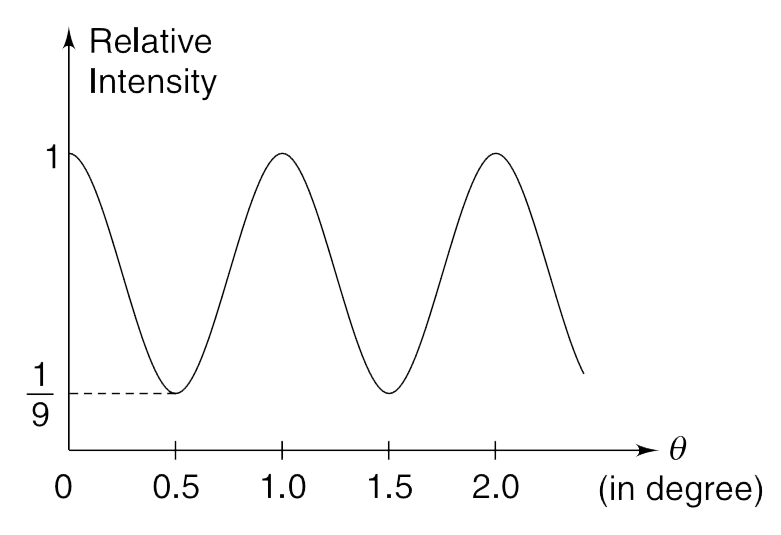
(a) Find separation d between the slits.
(b) Find the ratio of amplitudes of the two waves producing interference pattern on the screen.
View SolutionIn Young's double slit experiment, the distance between the two slits is 0.1 mm, the distance between the slits and the screen is 1 m and the wavelength of the light used is 600 nm. The intensity at a point on the screen is 75% of the maximum intensity. What is the smallest distance of this point from the central fringe ?
View Solution
