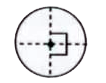
If a square of side R/2 is removed from a uniform circular disc of radius R as shown in the figure, the shift in centre of mass is
 Solution in Telugu
Solution in Telugu
R4π−1
R2(4π−1)
R3(4π−1)
R4(4π−1)
The correct Answer is:D
Step by step video & image solution for If a square of side R/2 is removed from a uniform circular disc of radius R as shown in the figure, the shift in centre of mass is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - PRACTICE SHEET (EXERCISE - I) LEVEL - I
7 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - PRACTICE SHEET (EXERCISE - I) LEVEL - II
1 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - LECTURE SHEET (EXERCISE - II)
4 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
Similar Questions
Three particle each of 1 kg mass are placed at corners of a right angled triangle AOB, 'O' being the origin of coordinate system (OA and OB along the x-direction and +ve y-direction). If OA = OB = 1m, the position vector of centre of mass (in metres) is
View SolutionA rope thrown over a pulley has ladder (of mass M - m) with a man of mass m on one of its ends and a counterbalancing mass M on its other end The man climbs with a velocity vr relative to a ladder. Pulley and rope are ideal. The velocity of centre of mass of the system is
View SolutionThe centre of mass of a non uniform rod of length L whose mass per unit length λ=Kx2L, where L is a constant and x is the distance from one end is
View SolutionThree liquids A,B and C having same specific heat and mass m , 2m and 3m have temperature 20∘C,40∘Cand60∘C respectively. Temperature of the mixture when :
Column -IColumn -IIA) A and B are mixed,is atP)35∘CB) A and C are mixed , is at Q)52∘CC) B and C are mixed , is at Q)50∘CD) A , B and C all three are mixed , is at S)45∘CT) None
View SolutionFour identical balls A,B,C and D are placed in a line on a frictionless horizontal surface. A and D are moved with same speed .u. towards the middle as shown. Assuming elastic collisions, find the final velocities.
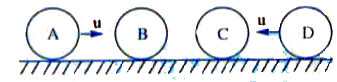
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the cirucmferences of the discs coincide. The centre of mass of the new disc is αR from the center of the bigger disc. The value of α is
View SolutionFrom a uniform circular dis of radius R , a circular dis of radius R//6 and having centre at a distance R//2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionA uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius (R)/(2) is removed from it. Then choose the correct option(s)
View SolutionIn the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
View SolutionFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

View SolutionFrom a uniform disc of radius R, an equilibatered triangle of side sqrt3R is cut as shown. The new position of centre of mass is:
View SolutionA circular disc of radius (R)/(4) is cut from a uniform circular disc of radius R. The centre of cut portion is at a distance of (R)/(2) from the centre of the disc from which it is removed. Calculate the centre of mass of remaining portion of the disc.
View SolutionFrom a uniform disc of radius R, a small disc of radius (R)/(2) is cut and removed as shown in the diagram. Find the center of mass of the remaining portion of the disc.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View Solution
