From a uniform disc of radius R, an equilibatered triangle of side √3R is cut as shown. The new position of centre of mass is:
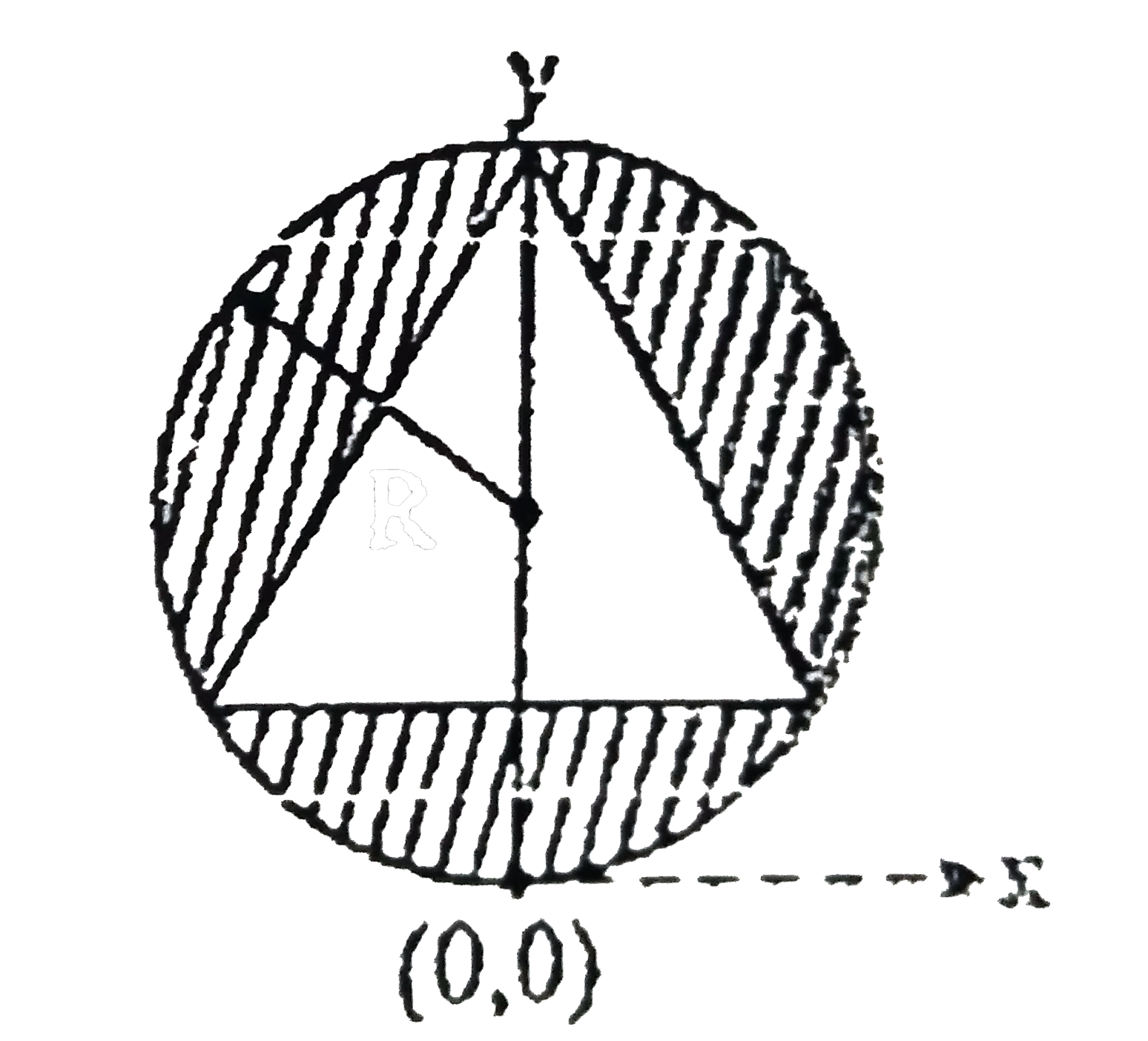
(0,0)
(0,R)
(0,√3R2)
none of these
Centre of mass remain mass remain at centre of the circle.
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
From a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View Solution
Knowledge Check
- Question 1 - Select One
From a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :
 A(0,0)B(0,R)C(0,√3R2)Dnone of these
A(0,0)B(0,R)C(0,√3R2)Dnone of these - Question 2 - Select One
From a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −
 A4R3(π−2)B2R3(π−2)C5R7(π−2)DR3(π−1)
A4R3(π−2)B2R3(π−2)C5R7(π−2)DR3(π−1) - Question 3 - Select One
A disc (of radius r cm) of uniform thickness and uniform density σ has a square hole with sides of length l=r√2cm. One corner of the hole is located at the centre of the disc and centre of the hole lies y-axis as shown. Then the y-coordinate of position of centre of mass of disc with hole (in cm) is.
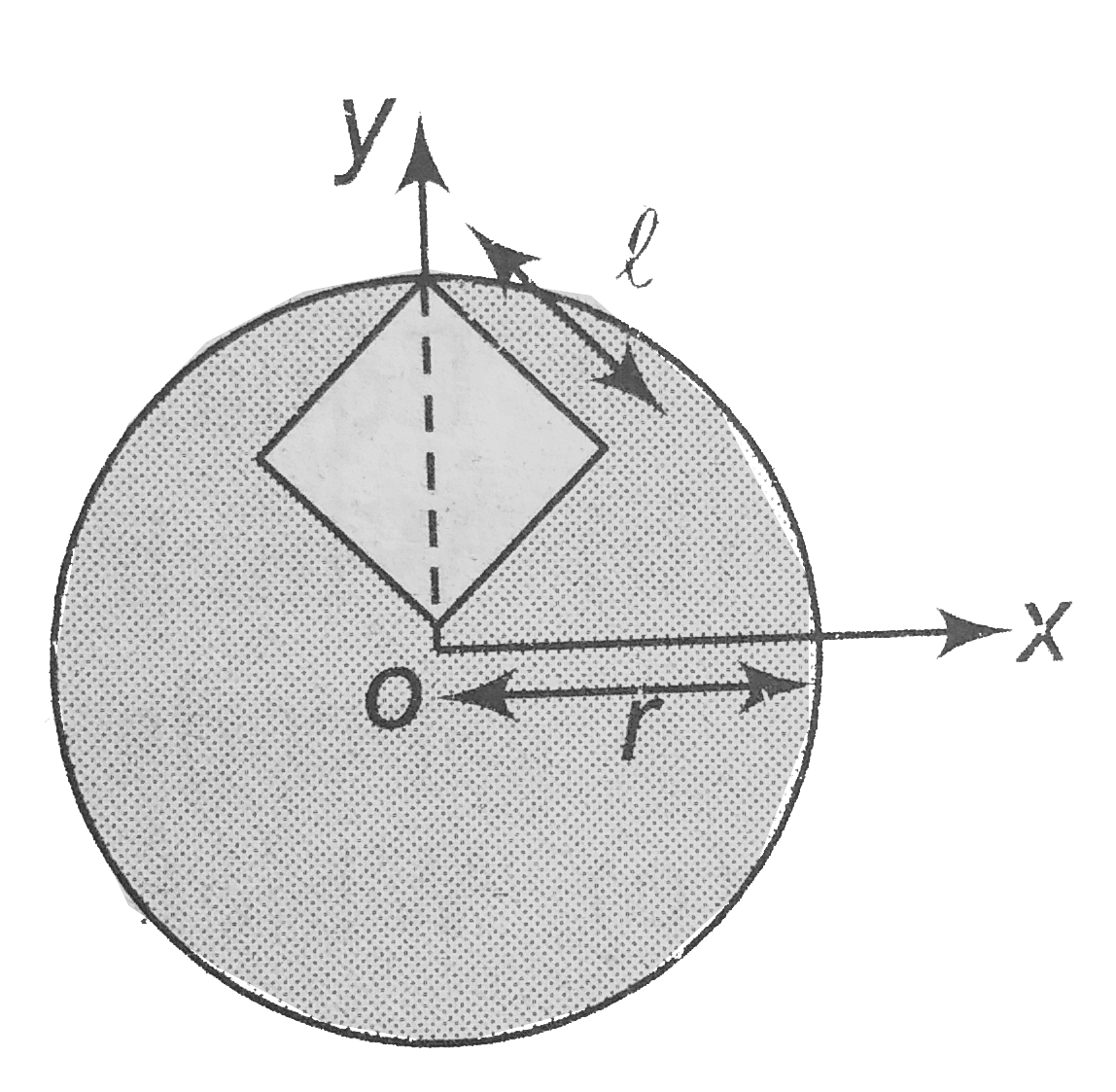 .A−r2(π−1/4)B−r4(π−1/4)C−r4(π−1/2)D−3r4(π−1/4)
.A−r2(π−1/4)B−r4(π−1/4)C−r4(π−1/2)D−3r4(π−1/4)
From a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.
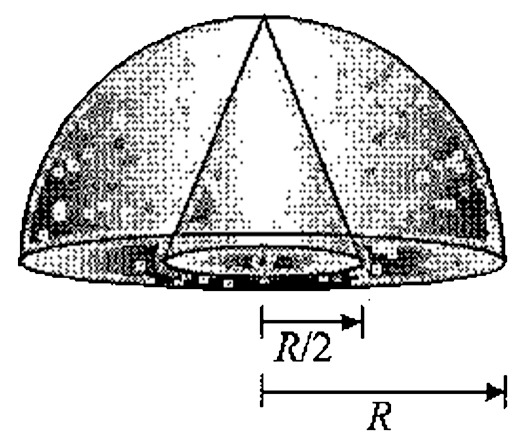 View Solution
View SolutionThe figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is
 View Solution
View SolutionA uniform sphere has radius R. A sphere of diameter R is cut from its edge as shown. Then the distance of centre of mass of remaining portion from the centre of mass of the original sphere is
 View Solution
View SolutionA uniform metal dise of radius R is taken and out of it a disc of diameter R is cut off from the end. The centre of the mass of the remaining part will be:
View SolutionFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
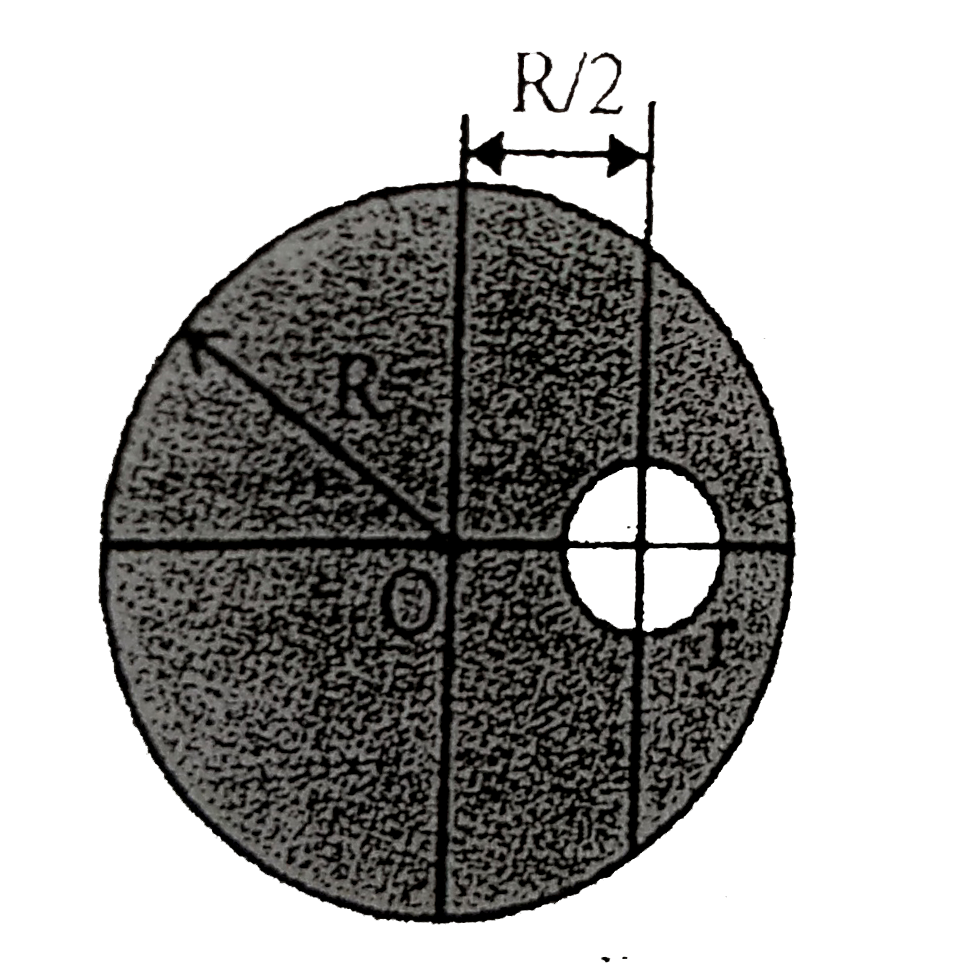 View Solution
View Solution

