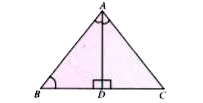
In D ABC, the bisector AD of A is perpendicular to side BC (see Fig. 7.27). Show that and is isosceles
The correct Answer is:AC
Step by step video solution for In D ABC, the bisector AD of A is perpendicular to side BC (see Fig. 7.27). Show that A B"\ "="\ "A C and DeltaA B C is isosceles by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In the adjoning figure of ΔABC,AD is the perpendicular bisector of side BC. The triangle ABC is :
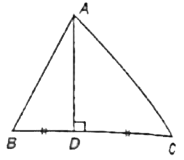 Aright angledBisoscelesCscaleneDequilateral
Aright angledBisoscelesCscaleneDequilateral
AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

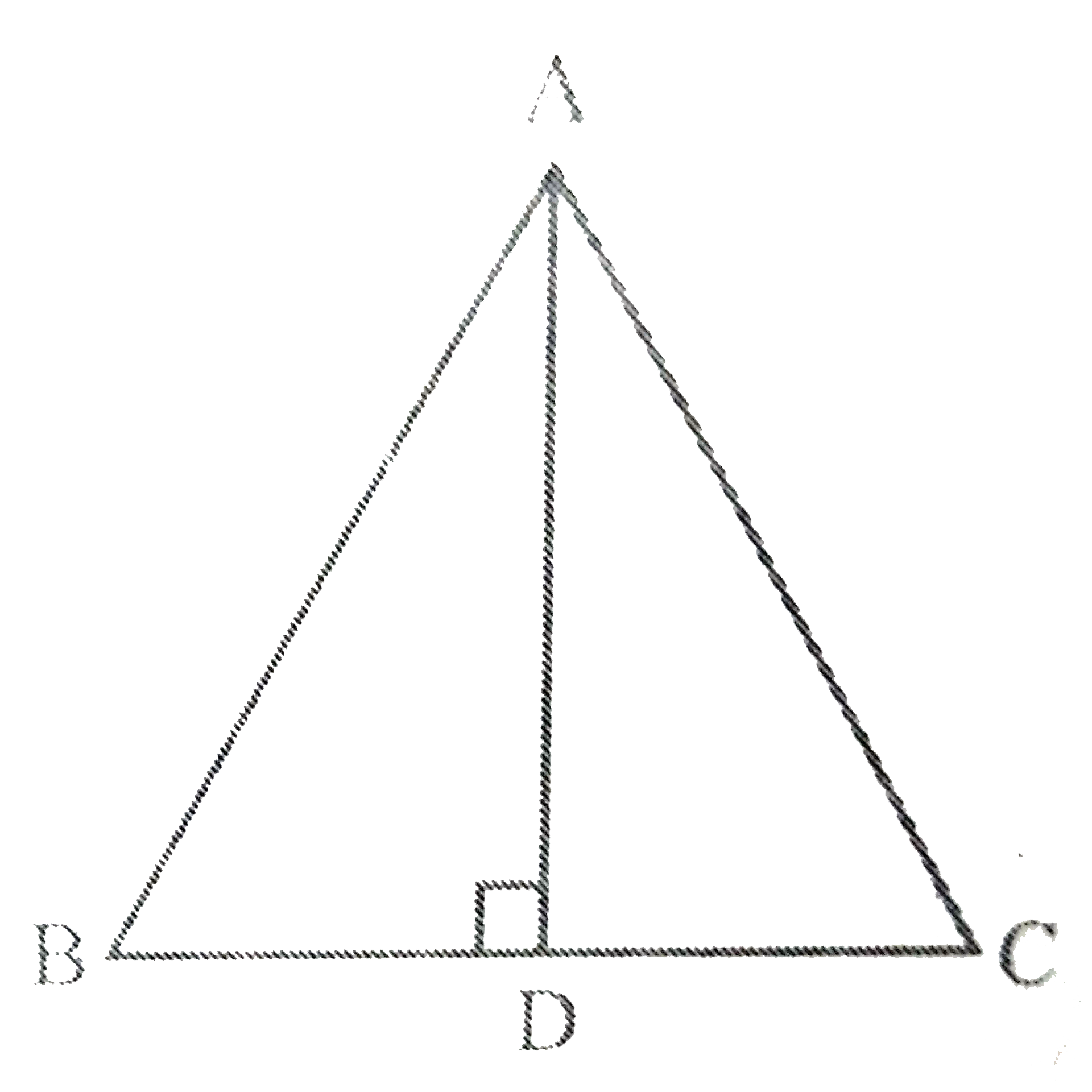
View SolutionIn ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABCis an isosceles triangle in which AB = AC.
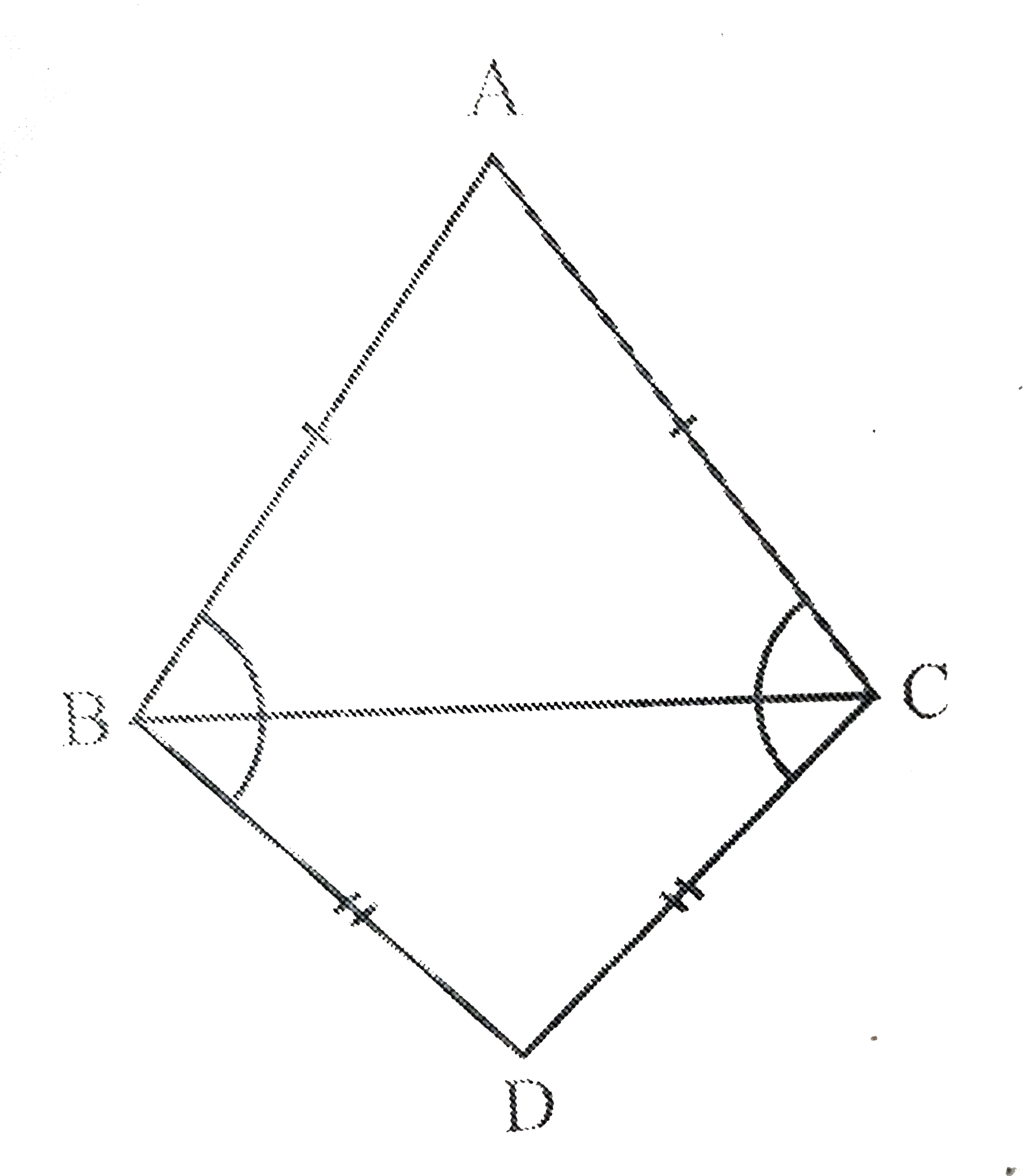
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD
View SolutionD is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionIn quadrilateral ACBD, AC = ADand AB bisects ∠A(see Fig. 7.16). Show that ΔABC≅ΔABD
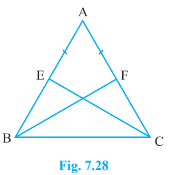
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
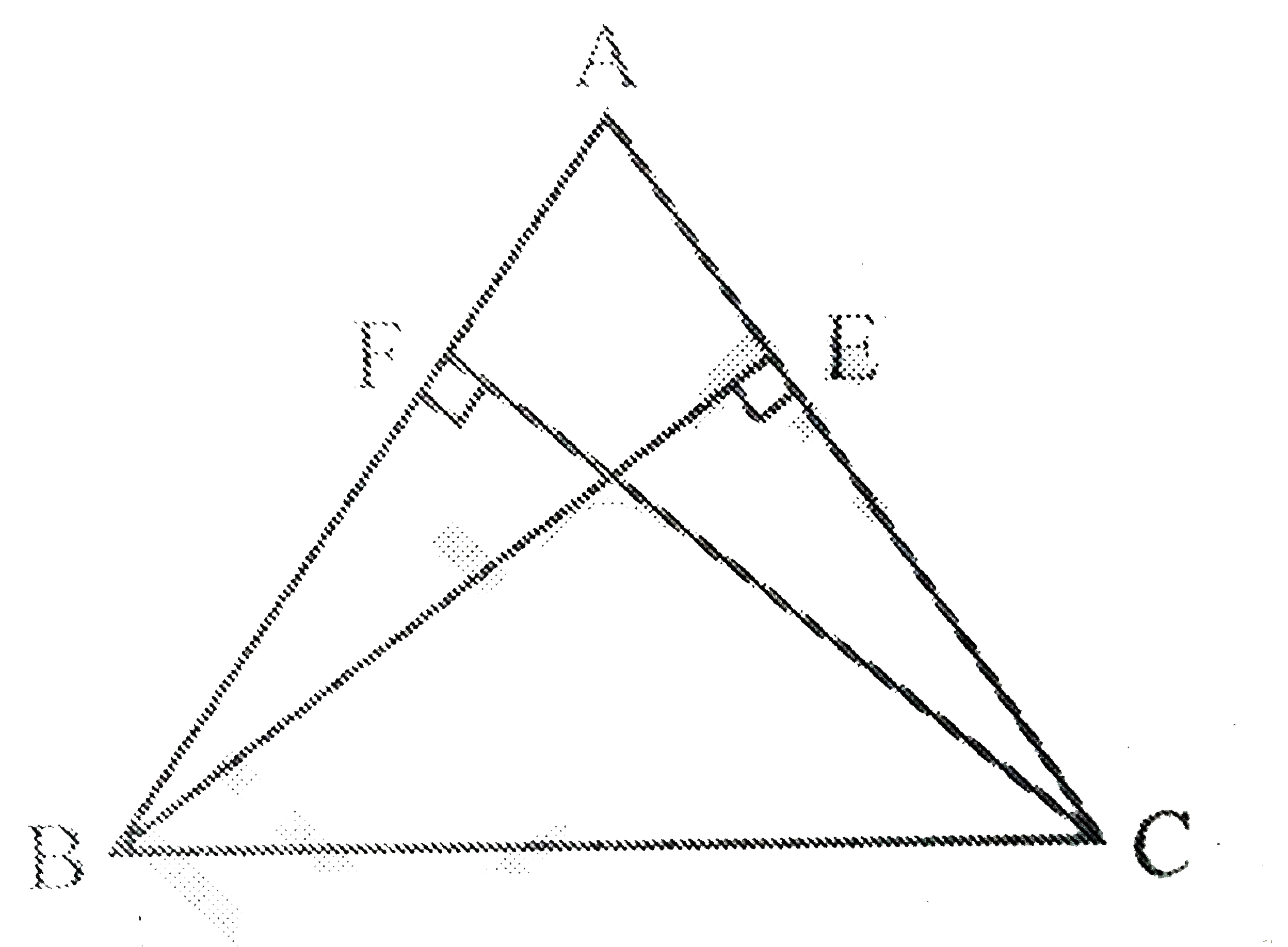
View Solution