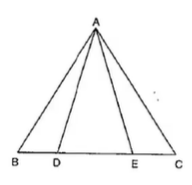
In an isosceles ΔABC with AB = AC, D and E are point on BC such that BE = CD. Show that AD = AE.
The correct Answer is:△ABE
Step by step video & image solution for In an isosceles DeltaABC with AB = AC, D and E are point on BC such that BE = CD. Show that AD = AE. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In a ΔABC, AB = AC and D is a point on AB, such that AD = DC = BC. Then, ∠BAC is
A40∘B45∘C30∘D36∘
In ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn a ΔABC,AB=AC=17cmD is a point on BC such that AD=15,CD=4cm, find BD=?
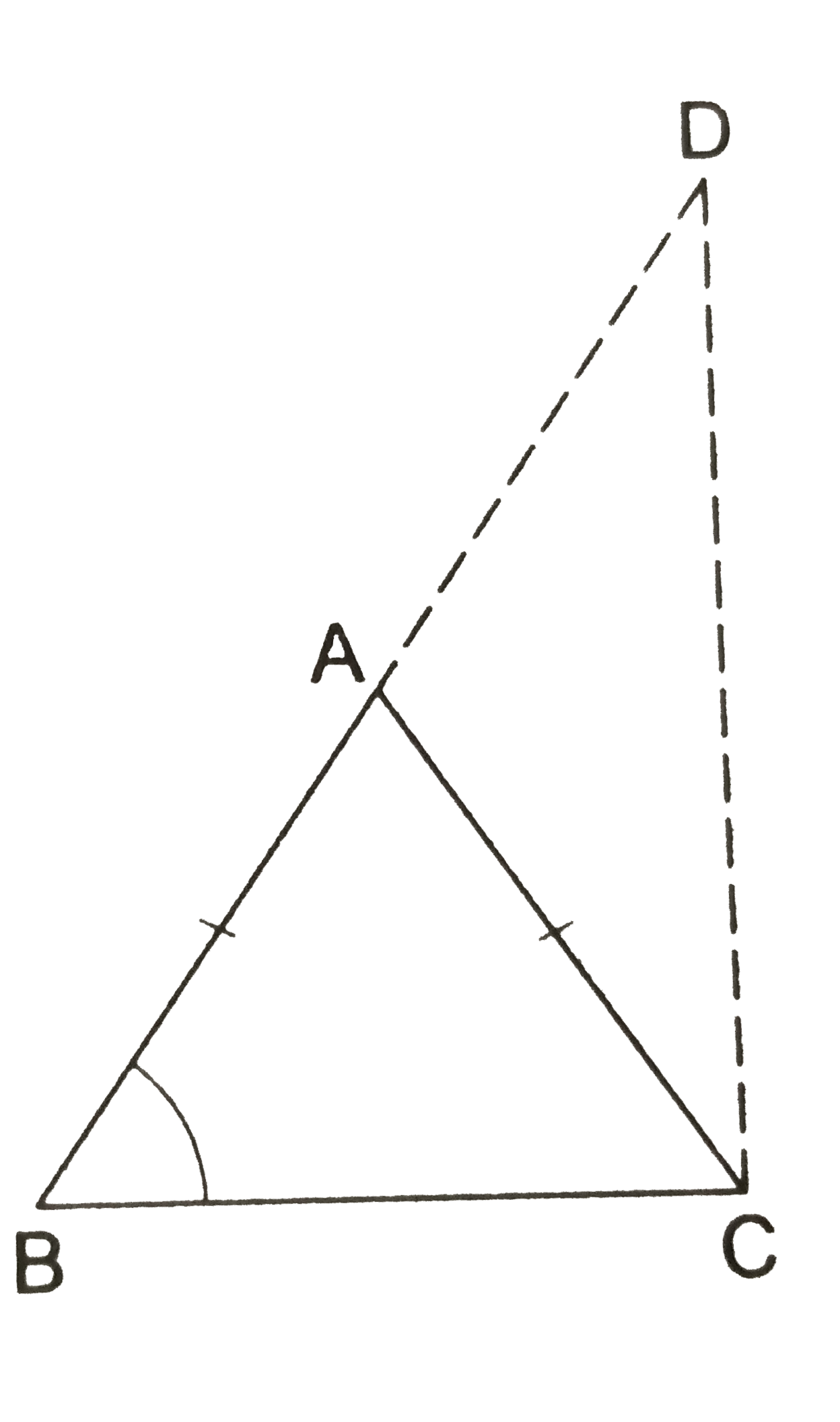
View SolutionΔABC is an isosceles triangle with AB = AC.
Side BA is produced to D such that AB = AD.
Prove that ∠BCD is a right angle.
View SolutionIn a ΔABC,AB=AC,D is a point on BC such that ∠BAD=50∘ and a point E on side AC such that AE = AD find ∠CDE.
View SolutionIn Figure, AC>AB and D is the point on AC such that AB=AD. Prove that BC>CD
View SolutionΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
View SolutionIn a ΔABC,AB=AC=17cmD is a point on BC such that AD=15,CD=4cm, find BD=?
View Solution