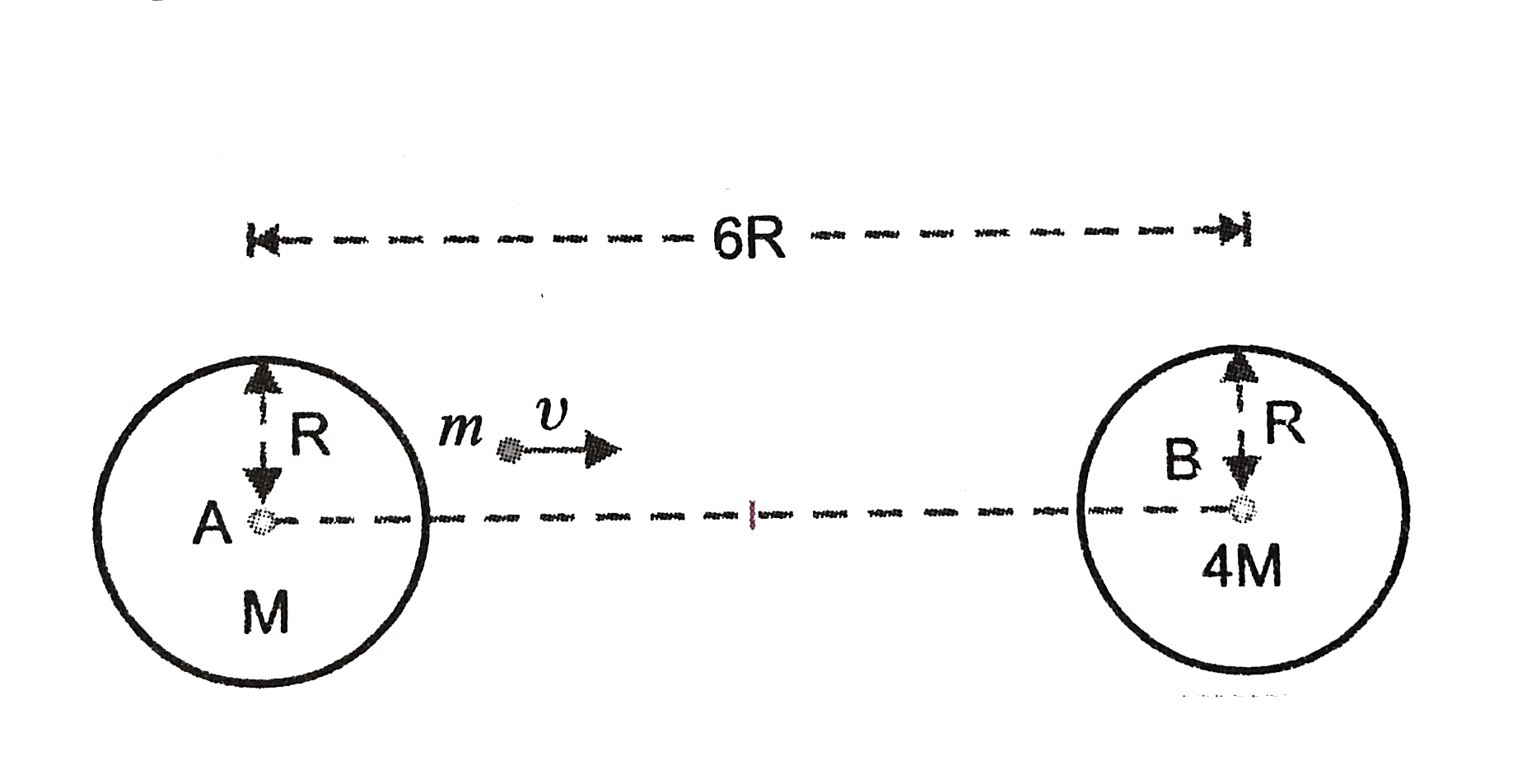
Two uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown . The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.

The projectile is acted upon by two mutually opposing gravitational forces of the two spheres. The neutral point N (see Fig. 8.10) is defined as the position where the two forces cancel each other exactly. If ON = r, we have
6 R - r = 2r
r = 2R or - 6R.
The neutral point r = – 6R does not concern us in this example. Thus ON = r = 2R. It is sufficient to project the particle with a speed which would enable it to reach N. Thereafter, the greater gravitational pull of 4M would suffice. The mechanical energy at the surface of M is
.
At the neutral point N, the speed approaches zero. The mechanical energy at N is purely potential.
From the principle of conservation of mechanical energy
or
A point to note is that the speed of the projectile is zero at N, but is nonzero when it strikes the heavier sphere 4 M. The calculation of this speed is left as an exercise to the students.
Topper's Solved these Questions
Similar Questions
Two uniform soild spheres of equal radii R but mass M and 4M have a centre to centre separation 6R, as shows in Fig. (a) The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of ten second. Obtain an expression for the minimum speed υ of the projectile so that it reaches the surface of second sphere.
View SolutionTwo uniform soild spheres of equal radii R but mass M and 4M have a centre to centre separation 6R, as shows in Fig. (a) The two spheres are held fixed. A projectile of massm is projected from the surface of the sphere of mass M directly towards the centre of teh second. Obtain an expression for the minimum speed υ of the projectile so that it reaches the surface of second sphere.

View Solution
Knowledge Check
Two uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown in figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.
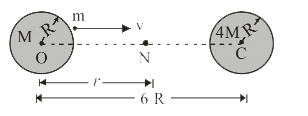 A√45GMRB√54GMRC√35GMRD√53GMR
A√45GMRB√54GMRC√35GMRD√53GMRThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
AGMa2BGMa3CGM2aDzeroA uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
A8GM2R2B2GM2√3R2C3GM22R2D√32GM2R2
Two uniform solid spheres of equal radii R, but mass M. and 4M have a centre to centre separation 6R, as shown in the figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the center of the second sphere. If the minimum speed v of the projectile so that it reaches the surface of the second sphere is √xGMyR, then find (x,+y).
'(##CEN_KSR_PHY_JEE_C10_038_Q05##)'
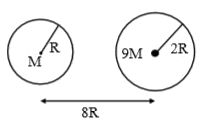
View SolutionSuppose two planets (spherical in shape) of radii R and 2R, but mass M and 9 M respectively have a centre to centre separation 8 R as shown in the figure. A satellite of mass 'm' is projected from the surface of the planet of mass 'M' directly towards the centre of the second planet. The minimum speed 'v' required for the satellite to reach the surface of the second planet is √a7GMR then the value of 'a' is ________.
[Given : The two planets are fixed in their position]
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionA particle of mass m is lying at the centre of a solid sphere of mass M and radius R. There is a turnel of negligible thickness, so that particle may escape. Find the minimum velocity required to escape the particle from the gravitational field of the sphere.
View SolutionA particle of mass m is lying at the centre of a solid sphere of mass M and radius R. There is a turnel of negligible thickness, so that particle may escape. Find the minimum velocity required to escape the particle from the gravitational field of the sphere.
View Solution
