The weight of an object in the coal mine, sea level and at the top of the mountain are respectively W1,W2andW3, then
W1<W2<W3
W1=W2=W3
W1<W2<W3
W1>W2>W3
The correct Answer is:A
Similar Questions
Knowledge Check
The weight of an object in the coal mine, sea level and at the top of the mountain are W1,W2 and W3 respectively, then
AW2>W1>W3BW1=W2=W3CW1<W2<W3DW1>W2>W3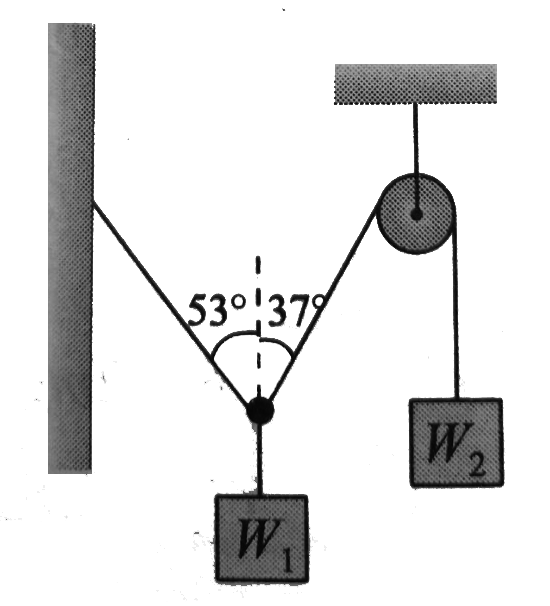
Two weights W1 and W2 in equilibrius and at rest are suspended as shown in figure. Then the ratio W1W2 is:A54B45C85Dnone of theseA density bottle weighs 120 g and 100 g when filled completely with oil ad water, respectively. If the weight of a empty density bottle is 40g, then arrange the following steps in sequence meant to solve the problem to get the density of oil
(A). The density of the oil
D=Mass of the oilWeight of the water=Mass of the oilMass of the water
=Weighht of oilWeight of the water=W3−W1W2−W1
(B). Let the weight of the bottle +oil=W3=120g
and the weight of the bottle+water =W2
100g, where bottle is completely filled with liquid, i.e., oil or water.
(C). Let the weight of the empty bottle=W1=40g
(D). The the weight of the oil ad water would be equal to (W3−W1)and(W2−W1), respectively.ACBDABABCDCBADCDDCBA
Why it is cooler at the top of a mountain than at sea level?
View SolutionIf W1andW2 are the weights of two reactants in any reaction, having their equivalent weights E1andE2 respectively, which of the following equations represents the law of equivalence correctly?
(a) W1E1=W2E2 (b) W1E2=W2E1 ( c ) W1W2=E1E2
View SolutionAngular speed of rotation of the earth is ω0. A train is running along the equator at a speed v from west to east. A very sensitive balance inside the train shows the weight of n object as W1. During the return journey when the train is running atsame speed from east to west the balance shows the weight of the object to be W2. Weight of the object when the train is at rest was shown to be W0 by the balance. Calculate W2–W1.
View Solution
Two weights W1 and W2 in equilibrius and at rest are suspended as shown in figure. Then the ratio W1W2 is:
View SolutionIf W1W2 and W3 represent the work done in moving a particle from A to B along three different paths 1.2 and3 respectively (asshown ) in the gravitational fieled of a point mass m, find the correct relation between W_(1) W_(2)andW_(3)
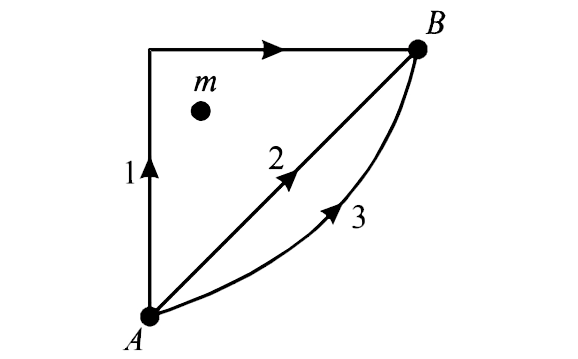
View Solution
