Let the speed of the planet at the perihelion P be VP and the sun-planet distance SP be rp. Relates (rp,VP) to the corresponding quantities at the aphelion (rA,VA). Will the planet take equal times to tranverse BAC and CPB ?
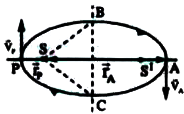
According to law of conservation of angular momentum. Angular of the planet at P = Angular momentum of the planet at A
⇒mVPrP=mVArA (or) VPVA=rArP Since rA>rP so VP>VA
Here area SBAC is greater than the area SCPB.
According to Kepler.s second law, as the arcal velocity of the planet is contant around the sun , i.e. equal areas are swept on equal times, hence the planet will take longer time to traverse BAC than CPB.
Topper's Solved these Questions
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -1A
262 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -1B
46 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II) PRACTICE SHEET (ADVANCED)Integer Type Questions
6 Videos
- HORIZONTAL CIRCULAR MOTIONBOOK - AAKASH SERIESCHAPTER - HORIZONTAL CIRCULAR MOTIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) Integer Type Questions)
3 Videos
Similar Questions
Let the speed of the planet at the perihelion P in figure be vP and the Sun planet distance SP be rP. Relater rP,vP to the corresponding quantities at the aphelion (rA,vA). Will the planet take equal times to transverse BAC and CPB?

View SolutionLet the speed of the planet at the perihelion P in figure be vP and the Sun planet distance SP be rP. Relater rP,vP to the corresponding quantities at the aphelion (rA,vA). Will the planet take equal times to transverse BAC and CPB?

View Solution
Knowledge Check
A: The speed of a planet is maximum at perihelion .
R : The angular momentum of a planet about centre of sun is conserved .AIf both Assertion & Reason are true . And the reason is the correct explanation of the assertion , then mark (1)BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion , then mark (2)CIf Assertion is true statement but Reason is false , then mark (3)DIt will move the same speed , tangentially to the spacecraftThe relation between Ip and Vp for a triode is
Ip=(0.124Vp−7.5)mA
Keeping the grid potential constant at 1 V , the value of rp will beA8kΩB4kΩC2kΩD8kΩA satellite of mass m orbits the earth in an elliptical orbit having aphelion distance ra and perihelion distance rp. The period of the orbit is T. The semi-major and semi-minor axes of the ellipse are ra+rp2 and √ρpra respectively. The angular momentum of the satellite is :
Amπ(ra+rp)√rarpTB2mπ(ra+rp)√rarpTCmπ(ra+rp)√rarp2TDmπ(ra+rp)√rarp4T
A speed of the palnet at the perihelion P be Vp and the sun -planet distance SP be rP as shown in fig. Relate {rp,vp} to the corresponding quantities at the aphelion {rA,VA}. Will the planet take equal times to traverse BAC and CPB?
View SolutionLet the speed of the planet at the perihelion P in figure be vP and the Sun planet distance SP be rP. Relater rP,vP to the corresponding quantities at the aphelion (rA,vA). Will the planet take equal times to transverse BAC and CPB?

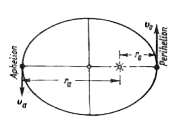
View SolutionThe point of an elliptical orbit closest to the Sun is called the perihelion, and the point most distant from it is called aphelion (Fig). Denoting the distance from the perihelion to the Sun by r0 and the velocity of the planet at the perihelion by v0 , find the radius of curvature of the orbit at the perihelion and at the aphelion, the distance from the aphelion to the Sun, and the velocity of the planet at the aphelion.
Prove that the motion of a planet in an elliptical orbit is only possible, if its total energy is negative.
View SolutionA: The speed of a planet is maximum at perihelion .
R : The angular momentum of a planet about centre of sun is conserved .
View SolutionA satellite of mass m orbits the earth in an elliptical orbit having aphelion distance ra and perihelion distance rp. The period of the orbit is T. The semi-major and semi-minor axes of the ellipse are ra+rp2 and √rpra respectively. The angular momentum of the satellite is: (A) 2mπ(rB+rp)√rarpT (B) mπ(ra+rp)√rarp2T (C) mπ(ra+rp)√rarp4T (D) mπ(ra+rp)√rarpT
View Solution
