The velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V−t graph.
V=K√s
dSdt=K√S∴S∫0dS√S=t∫0Kdt
∴2√S=KtandS=14K2t2
⇒V=dSdt=14K22t=12K2t
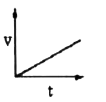
∴V∝t
∴ The V−t graph is a straight line passing through the origin
Similar Questions
Knowledge Check
- Question 1 - Select One or More
The velocity of a particle moving in the positive direction of x-axis veries as v=10√x. Assuming that at t=0, particle was at x=0
AThe initial velocity of the particle is zeroBthe initial velocity of the particle is 2.5ms.CThe accelration of the particle is 2.5ms2.DThe acceleration of the particle is 50ms2. - Question 2 - Select One
The velocity of a particle moving in the positive direction of X-axis varies as v=5√x. Assuming that at t = 0, particle was at x = 0. What is the acceleration of the particle ?
A12.5ms−2B7.5ms−2C5ms−2D2.5ms−2 - Question 3 - Select One
A particle constrained to move along x-axis given a velocity u along the positive x-axis. The acceleration ' a ' of the particle varies as a = - bx, where b is a positive constant and x is the x co-ordinate of the position of the particle . Then select the correct alternative(s): .
AThe maximum displacement of the particle from the starting point is u√bBThe particle will oscillate about the originCVelocity is maximum at the originDGiven data is insufficient to determine the exact motion of the particle.
The velocity of a particle moving in the positive direction of X-axis varies as v=5√x. Assuming that at t = 0, particle was at x = 0. What is the acceleration of the particle ?
View SolutionA particle constrained to move along x-axis given a velocity u along the positive x-axis. The acceleration ' a ' of the particle varies as a = - bx, where b is a positive constant and x is the x co-ordinate of the position of the particle . Then select the correct alternative(s): .
View SolutionThe dispkacement of particle is zero at t=0 and it is x , at t−t. It starts moving in the positive x-direction with a velocity which varices as v=k√x, where (k) is a constant. Show that velocity is directly proprtional to time.
View SolutionThe linear speed of a particle moving in a circle of radius R varies with time as v=v0−kt, where k is a positive constant. At what time the magnitudes of angular velocity and angular acceleration will be equal ?
View SolutionThe linear speed of a particle moving in a circle of radius R varies with time as v=v0−kt, where k is a positive constant. At what time the magnitudes of angular velocity and angular acceleration will be equal ?
View Solution

