A plane wave that falls on a barrier containing small circular opening of dimension d. What can be said about the behaviour of the wave if (i)λ<<d,(ii)λ=d,(iii)λ>>d
(i) When λ<<d i.e., wavelength of the wave is very very small when compared to the circular barrier or the diameter of the circular opening is lager than the wavelength of the waves coming out of the opening continue to move in straight lines, i.e., the ray approximation continues to be valid and we need not consider diffraction effects or wave nature. (ii) When λ=d i.e., the diameter of the opening is of the order of the wavelength, the waves spread out from the opening in all directions the wave nature is predominant. (iii) λ>>d i.e., if the circular opening is very small relative to the wavelength, the opening behaves as a point source of waves, and emits spherical waves. Diffraction is more pronounced. The above arguement is valid for all types of waves.
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - I)
18 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
20 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED ) Straight Objective Type Questions)
12 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
81 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
Figure shows four isotropic point sources of sound that are uniformly spaced on an x axis. The sources emit sound at the same wavelength λ and same amplitudes sm and they emit in phase. A point P is shown on the x axis. Assume that as the sound waves travel to P, the decrease in their amplitude is negligible. What multiple of sm is the amplitude of the net wave at P if distance d in the figure is (a)λ/4(b)λ/2and(c)λ ?
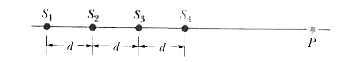
View SolutionA plane wave falls on a diffraction grating with a grating constant d0 at a glancing angle α. Prove that the resulting diffraction will be the same as when the wave falls normally on a grating with a grating constant of d = d0sinα.
View Solution
Knowledge Check

In the figure the intensity of waves arriving at D from two coherent sources S1 and S2 is I0 The wavelength of the wave is λ=4m. Resultant intensity at D will be:A4I0BI0C2I0Dzero_E01_037_Q01.png)
Two coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 3λ the light is collected on a screen S which is placed at a distance D(>>λ) from the slits the smallest distance x such that the P is a maxima.A√3DB√8DC√5DD√5D2de Broglie (1924) predicted that small particles such as electrons should show wave -like properties along with paticle character. The wave length(λ) associated with particle of mass m and moving with velocity v is given as λ=hmv where 'h' is plank's constant. The wave nature was confirmed by Davisson and Germer's experiment and modified equation for calculation of λ can be given as:
λ=−h√2Em where E= kinetic energy of particle.
λ=h√2dVm, where d= change of particle accelerated potnetial of V volt.
Velocity of d e-Broglie's waves is given byAc2vBhvmcCmc2hDvλ
Consider a coaxial system of two thin convex lenses of focal length f each separated by a distance d. Draw ray diagrams for image formation corresponding to an object at infinity placed on the principal axis in the following cases: (a) d<f,(b)d=f, (c ) f<d<2f, (d) d=2f, and (e) d>2f. Indicate the nature of the combination (concave, convex or plane) in each case.
View SolutionConsider a coaxial system of two thin convex lenses of focal length f each separated by a distance d. Draw ray diagrams for image formation corresponding to an object at infinity placed on the principal axis in the following cases: (a) d<f,(b)d=f, (c ) f<d<2f, (d) d=2f, and (e) d>2f. Indicate the nature of the combination (concave, convex or plane) in each case.
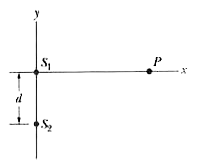
View SolutionFigure shows two point sources S1 and S2 that emit sound of wavelength λ = 3.00 m. The emissions are isotropic and in phase, and the separation between the sources is d = 16.0 m. At any point P on the x axis, the wave from S1 and the wave from S2 interfere. When P is very far away (x≈0) , what are (a) the phase difference between the arriving waves from S1 and S2 and (b) the type of interference they produce? Now move point P along the x axis toward S1. (c ) Does the phase difference between the waves increase or decrease? At what distance x do the waves have a phase difference of (d) 0.50λ,(e)1.00λ, and (f) 1.50λ?
View SolutionFigure shows two, identical narow slits S1 and S2. A very small completely strip is placed at distacne y from the point C. C is the point on the screen equidistant from S1 and S2. Assume λ<<d<<D, where λ,d and D have usual meaning. When S2 is covered the force due to light acting on strip is f and when both slits are opened the force acting on strip is 2f. Find the minimum positive y(<<D) coordinate (in cm) of the strip if λDd=4cm

View SolutionThe p.d.f of continuous random variable X is given by f(x)=x8,0<x<4=0 otherwise. Find (i) P(X<2)(ii)P(2<X≤3)(iii)P(X>3.)
View Solution
