Figure shows position and velocities of two particles moving under mutual gravitational attraction in space at time t=0. The position of centre of mass after one second is
Figure shows position and velocities of two particles moving under mutual gravitational attraction in space at time t=0. The position of centre of mass after one second is

A

x = 4 m

B

x = 6 m

C

x = 8 m

D

x = 10 m

Text Solution
Verified by Experts

The correct Answer is:D

As →Fext=0,∴→aCM=0
→vCM=2×8ˆi−3×2ˆi2+3=2ˆi,XCM=2×2+3×122+3=8
As →vCM is constant , so centre of mass will move 2m in one second
∴ x = 8 + 2 = 10 m

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 11PHYSICSRIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The figure shows the positions and velocity of two particle. If the paritcle move under the mutual attraction of each other, then the position of centre of mass at t=1s is :-
    ocr_image

    Ax=5m
    Bx=6m
    Cx=3m
    Dx=2m

  • Figure shows the position of a particle moving on the x - axis as a function of time
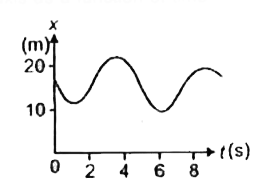    ocr_image

    AThe particle has come to rest 4 times
    BThe velocity at t = 8 s is negative
    CThe velocity remains positive for t = 2 s to t = 6 s
    DThe particle moves with constant velocity.

  • Figure shows the position of a particle moving on the X-axis as a function of time.
    ocr_image

    AThe particle has come to rest 6 times
    BThe maximum speed is at t=6 s.
    CThe velocity remains positive for t=0 to t=6s.
    DThe average velocity for the total period shown is negative