In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
60cm
50cm
40cm
20cm
The correct Answer is:C
To solve the problem regarding the meter bridge experiment, we will follow these steps:
Step 1: Understand the Setup
In a meter bridge, we have a wire of length 100 cm, and we connect two resistances on either side of a bridge. The left gap has an unknown resistance X and the right gap has a known resistance R.
Step 2: Set Up the Ratio
According to the problem, the ratio of the left gap resistance to the right gap resistance is given as 2:3. This can be expressed mathematically as:
XR=23
From this, we can express X in terms of R:
X=23R
Step 3: Apply the Principle of the Meter Bridge
The principle of the meter bridge states that the ratio of the resistances is equal to the ratio of the lengths of the bridge. If L1 is the length from point A to the balance point B, then the remaining length from B to the end of the bridge (100 cm) is 100−L1.
According to the principle:
XR=L1100−L1
Step 4: Substitute the Value of X
Substituting X=23R into the equation gives:
23RR=L1100−L1
This simplifies to:
23=L1100−L1
Step 5: Cross-Multiply to Solve for L1
Cross-multiplying gives:
2(100−L1)=3L1
Expanding this results in:
200−2L1=3L1
Step 6: Combine Like Terms
Rearranging the equation yields:
200=3L1+2L1
200=5L1
Step 7: Solve for L1
Dividing both sides by 5 gives:
L1=2005=40 cm
Conclusion
Thus, the balance point from point A is at 40 cm.
In a meter bridge, we have a wire of length 100 cm, and we connect two resistances on either side of a bridge. The left gap has an unknown resistance X and the right gap has a known resistance R.
According to the problem, the ratio of the left gap resistance to the right gap resistance is given as 2:3. This can be expressed mathematically as:
XR=23
From this, we can express X in terms of R:
X=23R
The principle of the meter bridge states that the ratio of the resistances is equal to the ratio of the lengths of the bridge. If L1 is the length from point A to the balance point B, then the remaining length from B to the end of the bridge (100 cm) is 100−L1.
XR=L1100−L1
Substituting X=23R into the equation gives:
23RR=L1100−L1
This simplifies to:
23=L1100−L1
Cross-multiplying gives:
2(100−L1)=3L1
Expanding this results in:
200−2L1=3L1
Rearranging the equation yields:
200=3L1+2L1
200=5L1
Dividing both sides by 5 gives:
L1=2005=40 cm
Thus, the balance point from point A is at 40 cm.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - POTENTIOMETER7videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - HOTS8videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - WHEATSTONE BRIDGE6videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Assertion And Reason30videos
COMMUNITCATION SYSTEMS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason15videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
In a meter-bridge experiment with a resistance R1 in left gap and a resistance X in a right gap. null point is obtained at 40cm from the left emf. With a resistance R2 in the left gap, the null point is obtainned at 50cm from left hand. Find the position of the left gap is containing R1 and R2 (i) in series and (ii) in parallel.
View SolutionIn metre bridge experiment, with a standard resistance in the right gap and a resistance coil dipped in water (in a beaker) in the left gap, the balancing length obtained is '1'. If the temperature of water is increased, the new balancing
View SolutionIn a meter bridge experment, the value of unknown resistance is 2Ω. To get tehbalancing point at 40 cm distance form the same end, the resistance in the resistance box will be :
View SolutionIn meter bridge experiment if, resistance S in resistance box =300Ω then the balanced length is found to be 25.0cm from end A. The diameter of unknown wire is 1mm and length of unknown wire is 31.4cm. The specific resistivity of the wire should be
View SolutionIn a meter bridge, null point is at l=33.7cm, when the resistance S is shunted by 12Ω resitance the null point is found to be shifted by a distance of 18.2cm. The value of unknown resistance R should be
 View Solution
View SolutionIn a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
View SolutionIn a metre bridge experiment to determine unknown resistance of a coil, how is position of the null point affected if:
(i) Galvanometer and cell are interchanged?
(ii) Known and unknown resistances are interchanged?View SolutionAn unknown resistance R1 is connected is series with a resistance of 10Ω. This combination is connected to one gap of a meter bridge, while other gap is connected to another resistance R2. The balance point is at 50cm Now , when the 10Ω resistance is removed, the balanced point shifts to 40cm Then the value of R1 is.
View SolutionAn unknown resistance R1 is connected is series with a resistance of 10Ω. This combination is connected to one gap of a meter bridge, while other gap is connected to another resistance R2. The balance point is at 50cm Now , when the 10Ω resistance is removed, the balanced point shifts to 40cm Then the value of R1 is.
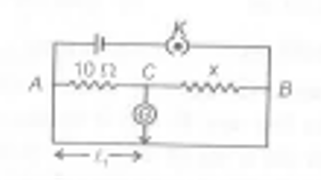
View SolutionThe resistance in two arms of the meter bridge is 10Ω and x respectively. The balance length is l1from left. Now the resistance of 10Ω is shunted with another resistor of resistance equal to unknown resistance x then new balance point is 0.75l1 The value of resistance x is
 View Solution
View Solution

