An ideal gas with the adiabatic exponent y goes through a direct (clockwise) cycle, consisting of adiabatic, isobaric and isochoric lines. Find the efficiency of the cycle if in the adiabatic process the volume of the ideal gas increases n fold.
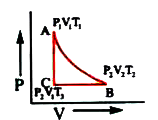
1−γ(n−1)nγ−1
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - NUMERICAL EXERCISE (LEVEL-2)
35 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
7 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
24 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
- THERMOMETRY BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11 Videos
Similar Questions
An ideal gas with the adiabatic exponent γ goes through a direct (clockwise) cycle conisting of adiabatic, isobaric, and isochoric lines. Find the efficiency of the cycle if in the adiabatic process the volume of the ideal gas.
(a) increases n-fold ,
(b) decreases n-fold.
View SolutionAn ideal gas whose adiabatic exponent equals γ goes through a cycle consisting of two isochoric and two isobaric lines. Find the efficiency of such a cycle, if the absolute temperature of the gas rises n times both in a isochoric heating and in the isobaric expansion.
View Solution
Knowledge Check
Helium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)
 A15.4%B9.1%C10.5%D12.5%
A15.4%B9.1%C10.5%D12.5%Helium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)
 A15.4%B9.1%C10.5%D12.5%
A15.4%B9.1%C10.5%D12.5%
An ideal gas with the adiabatic exponent γ goes through a cycle (Fig. 2.3) within which the absolute temperature varies τ−fold. Find the efficiency of this cycle.
 .
.
View SolutionAn ideal gas is expended adiabatically then
View SolutionAn ideal gas is expended adiabatically then
View SolutionHelium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)

View SolutionHelium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)

View SolutionCalculate the efficiency of a cycle consisting of isothermal, isobaric, and isochoric line, if in the isothermal process the volume of the ideal gas with the adiabatic exponent γ.
(a) increased n−fold ,
(b) decreases n−fold.
View Solution
