Fig. (1) shows the graphs of elongation versus temperature for two different metals. If these metals be employed to form a straight bimetallic strip of thickness 6cm and heated it bends in the form of an arc, the radius of curvature changing with temperature approximately as shown in fig(2). The linear expansivities of the two metals are
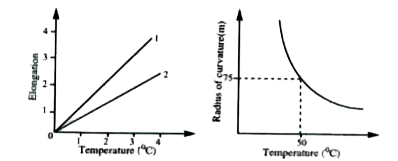
Fig. (1) shows the graphs of elongation versus temperature for two different metals. If these metals be employed to form a straight bimetallic strip of thickness 6cm and heated it bends in the form of an arc, the radius of curvature changing with temperature approximately as shown in fig(2). The linear expansivities of the two metals are

A

24×10−6/°Cand12×10−6/°C

B

20×10−6/°Cand10×10−6/°C

C

18×10−6/°Cand10−6/°C

D

16×10−6/°Cand8×10−6/°C

Text Solution
Verified by Experts

The correct Answer is:D

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 11PHYSICSPROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • ocr_image
    Figure. Shows the graphs of elongation versus temperature for two different metals. If these metals are employed to form a straight bimetallic strip of thickness 6 cm and heated, it bends in the form of an arc, the radius of cuvature chaging with temperature approximately as shown in the figure. The linear expansivities of the two metals are

    A24×10−6/∘C and 12×10−6/∘C
    B20×10−6/∘C and 10×10−6/∘C
    C18×10−6/∘C and 9xx10^(-6)//^@C
    D16×10−6/∘C and 8×10−6/∘C

  • ocr_image
    The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will be

    AαA=3×10−6/∘C,500∘C
    BαA=3×10−6/∘C,222.22∘C
    CαA=27×10−6/∘C,500∘C
    DαA=27×10−6/∘C,222.22∘C

  • Bars of two different metals are bolted together , as shown in figure. The distance x does not change with temperature if :-
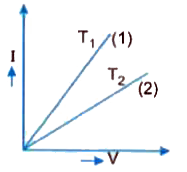
    ocr_image

    AlAlB=αAαB
    BlAlB=αBαA
    ClA2lB2=αAαB
    DlA2lB2=αBαA