A radioactive nucleus X decays to nucleus Y which further decays to a stable nucleus Z as given below Xλx=0,1sec−1−−−−−−−−→Yλy=130sec−1−−−−−−−→Z (stable). Initially the sample contains nuclei of X only and its population is N0=1020 . Further the population of Y as function of time is given by
NY(t)=N0λXλX−λY(e−λyt−e−λxt)
(a) If NX,NYandNZ represent population of X, Y and Z respectively at any instant of time t . Find dNYdt
(b) Find the time at which population of Y is maximum
(c) Find the population of X at instant when NY is maximum
The correct Answer is:(a) 0.1Nx−NY30 (b) 15In3 (c) 1020√39
Similar Questions
A radioactive nucleus X decays to a nucleus Y with a decay constant λX=0.1s−1, Y further decays to a stable nucleus Z with a decay constant
λY=1/30s−1. Initially, there are only X nuclei and their number is N0=1020. Set up the rate equations for the populations of X, Y and Z. The population of Y nucleus as a function of time is given by NY(t)={N0λX/(λX−λY)}[exp(−λYt)−exp(−λXt)].
Find the time at which NY is maximum and determine the population X and Z at that instant.
View SolutionA radioactive nucleus X decays to a nucleus Y with a decay constant λX=0.1s−1, Y further decays to a stable nucleus Z with a decay constant
λY=1/30s−1. Initially, there are only X nuclei and their number is N0=1020. Set up the rate equations for the populations of X, Y and Z. The population of Y nucleus as a function of time is given by NY(t)={N0λX/(λX−λY)}[exp(−λYt)−exp(−λXt)].
Find the time at which NY is maximum and determine the population X and Z at that instant.
View Solution
Knowledge Check
An unstable nucleus X can decay into two stable nuclie Y and Z A sample containing only X is taken at t=0 Three graphs loge(Nx vs t,Nx, vs t and Nz vs t are drawn as shown below Here Nx,Ny and Nz represent number of nuclei of X,Y and Z repectively at any instant. t
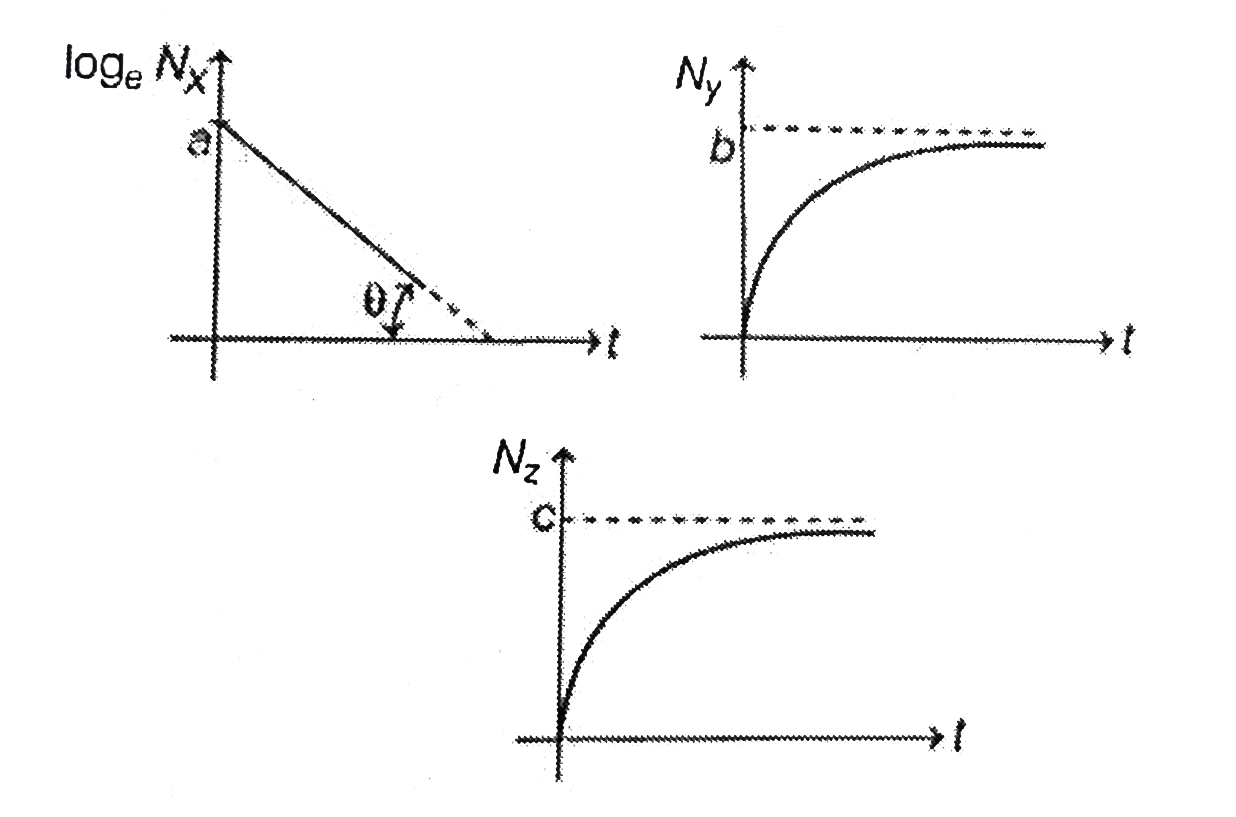
Choose the correct choice (s) from the following :ADecay constant for decay of X into Y is btanθeaBecay constant for decay of X into Z is ctanθeaCNumber of nuclei of X at t=0-is eaDHalf-life of nuclei X is 1tanθNucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
At0=1λ1ln[3λ12λ2]Bt0=1λ1lm[λ1λ2]Ct0=1λ1ln[2λ13λ2]Dt0=1λ2ln[3λ12λ2]A radioactive element A of decay constant λA decays into another radioactive element B of decay constant λB. Initially the number of active nuclei of A was N0 and B was absent in the sample. The maximum number of active nuclei of B is found at t=2. In 2/λA. The maximum number of active nuclei of B is
AN04BλAλBN0e−λBtCλAλBN04DNone of these
A radioactive nucleus Xdecay to a nucleus Y with a decay with a decay Concept λx=0.1s−1,γ further decay to a stable nucleus Z with a decay constant λy=1/30s−1 initialy, there are only X nuclei and their number is N0=1020 set up the rate equations for the population of X9)YandZ The population of Y nucleus as a function of time is givenby Ny(1)=N0λxl(λx−λy))(exp(−λy1))F∈dthetimeatwhichN_(y)ismaxiμmanddeterminethepop∗–––ionX and Y at that instant.
View SolutionAn unstable nucleus X can decay into two stable nuclie Y and Z A sample containing only X is taken at t=0 Three graphs loge(Nx vs t,Nx, vs t and Nz vs t are drawn as shown below Here Nx,Ny and Nz represent number of nuclei of X,Y and Z repectively at any instant. t

Choose the correct choice (s) from the following :
View SolutionA radioactive isotope X decays into a stable nucleus Y. Draw graphs showing the variation of rate of formation of Y versus time and the variation of population of Y versus time. Initial population of Y is zero.
View SolutionNucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
View SolutionNucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
View Solution
