Graph of logK and 1/T was given for which valuue of slope is -10000 K if T is 500K and rate constant is at which temperature value rate constant will be
To solve the problem, we will use the Arrhenius equation and the relationship between the rate constants at different temperatures. Here's a step-by-step breakdown of the solution:
Step 1: Understand the Arrhenius Equation
The Arrhenius equation is given by:
k=Ae−EaRT
Where:
- k = rate constant
- A = pre-exponential factor
- Ea = activation energy
- R = universal gas constant (8.314 J/mol·K)
- T = temperature in Kelvin
Step 2: Convert to Logarithmic Form
Taking the logarithm of both sides, we can express it as:
logk=logA−Ea2.303RT
Step 3: Identify the Slope
From the problem, we know that the slope of the graph of logk vs. 1T is:
m=−Ea2.303R=−10000K
Step 4: Calculate Activation Energy
Using the slope, we can rearrange to find Ea:
Ea=−m⋅2.303R
Substituting the values:
Ea=10000⋅2.303⋅8.314
Calculating this gives:
Ea≈190.2kJ/mol
Step 5: Set Up the Equation for Two Temperatures
Now we need to find the temperature T2 at which the rate constant k2=10−4 when k1=10−5 at T1=500K.
Using the Arrhenius equation in the form:
k2k1=e−EaR(1T2−1T1)
Step 6: Substitute Known Values
Substituting k1, k2, T1, and Ea:
10−410−5=e−1902008.314(1T2−1500)
This simplifies to:
10=e−1902008.314(1T2−1500)
Step 7: Take the Natural Logarithm
Taking the natural logarithm of both sides:
ln(10)=−1902008.314(1T2−1500)
Step 8: Solve for T2
Rearranging gives:
1T2−1500=−8.314ln(10)190200
Calculating ln(10)≈2.303:
1T2−1500=−8.314⋅2.303190200
Calculating the right-hand side:
1T2=1500−0.0001T2
Step 9: Final Calculation
Cross-multiplying and solving for T2:
T2≈526.3K
Final Answer
The temperature at which the rate constant will be 10−4 is approximately 526.3 K.
---
The Arrhenius equation is given by:
k=Ae−EaRT
Where:
- k = rate constant
- A = pre-exponential factor
- Ea = activation energy
- R = universal gas constant (8.314 J/mol·K)
- T = temperature in Kelvin
Taking the logarithm of both sides, we can express it as:
logk=logA−Ea2.303RT
From the problem, we know that the slope of the graph of logk vs. 1T is:
m=−Ea2.303R=−10000K
Using the slope, we can rearrange to find Ea:
Ea=−m⋅2.303R
Substituting the values:
Ea=10000⋅2.303⋅8.314
Calculating this gives:
Ea≈190.2kJ/mol
Now we need to find the temperature T2 at which the rate constant k2=10−4 when k1=10−5 at T1=500K.
k2k1=e−EaR(1T2−1T1)
Substituting k1, k2, T1, and Ea:
10−410−5=e−1902008.314(1T2−1500)
This simplifies to:
10=e−1902008.314(1T2−1500)
Taking the natural logarithm of both sides:
ln(10)=−1902008.314(1T2−1500)
Rearranging gives:
1T2−1500=−8.314ln(10)190200
Calculating ln(10)≈2.303:
1T2−1500=−8.314⋅2.303190200
1T2=1500−0.0001T2
Cross-multiplying and solving for T2:
T2≈526.3K
The temperature at which the rate constant will be 10−4 is approximately 526.3 K.
Similar Questions
For a reaction graph between logK vs 1T is as with slope = -10,000.

At temperature 500K rate constant k = 10−5 .
Find the temperature in K at which rate constant = 10−4
View SolutionWhich one of the following given graphs represents the variation of rate constant (k) with temperature (t) for an endothermic reaction ?
View Solution
Knowledge Check
Graph between log k and 1/T [where K is rate constant in s−1 and T is the temperature (in K) is a straight line with Hence, Ea will be
 A2.303×2 calB22.303calC2 calDNone of these
A2.303×2 calB22.303calC2 calDNone of theseFor a reaction, activation energy (Ea) =0 and rate constant, k=1.5x104s−1 at 300 K. What is the value of rate constant at 320 K'?
A3.2x106s−1B3.2x104s−1C1.5x104s−1D6.4x108s−1Which of the following graph is incorrect for variation of rate constant (K) with temperature for a reaction obeying Arrhenius equation ?
A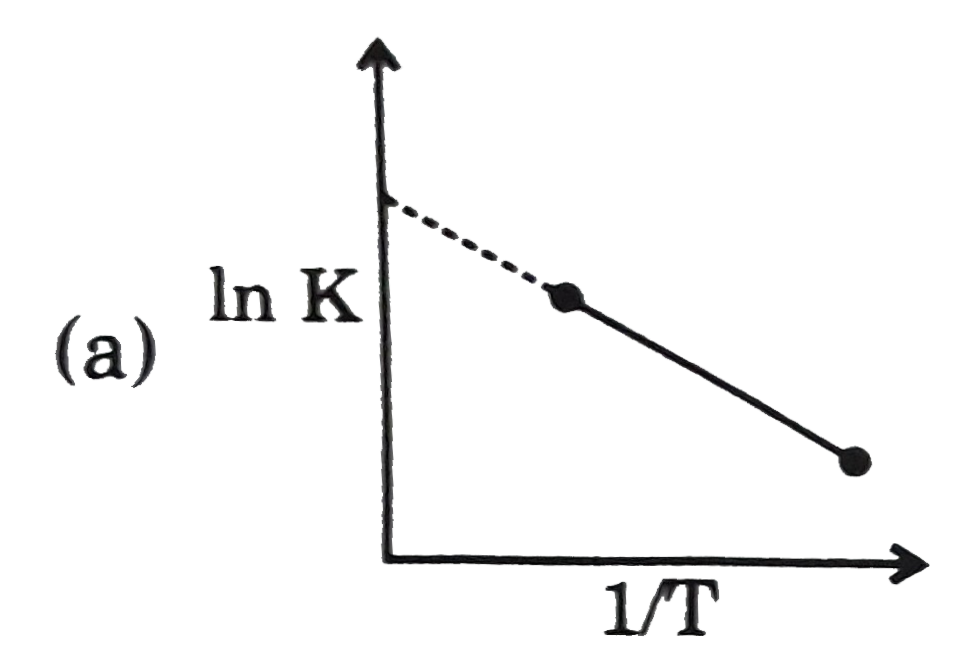 B
B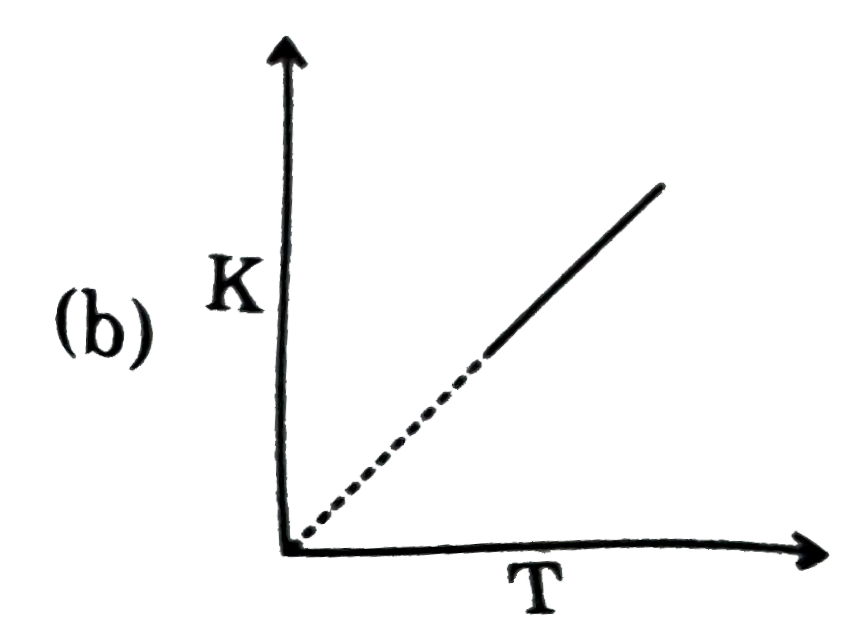 C
C D
D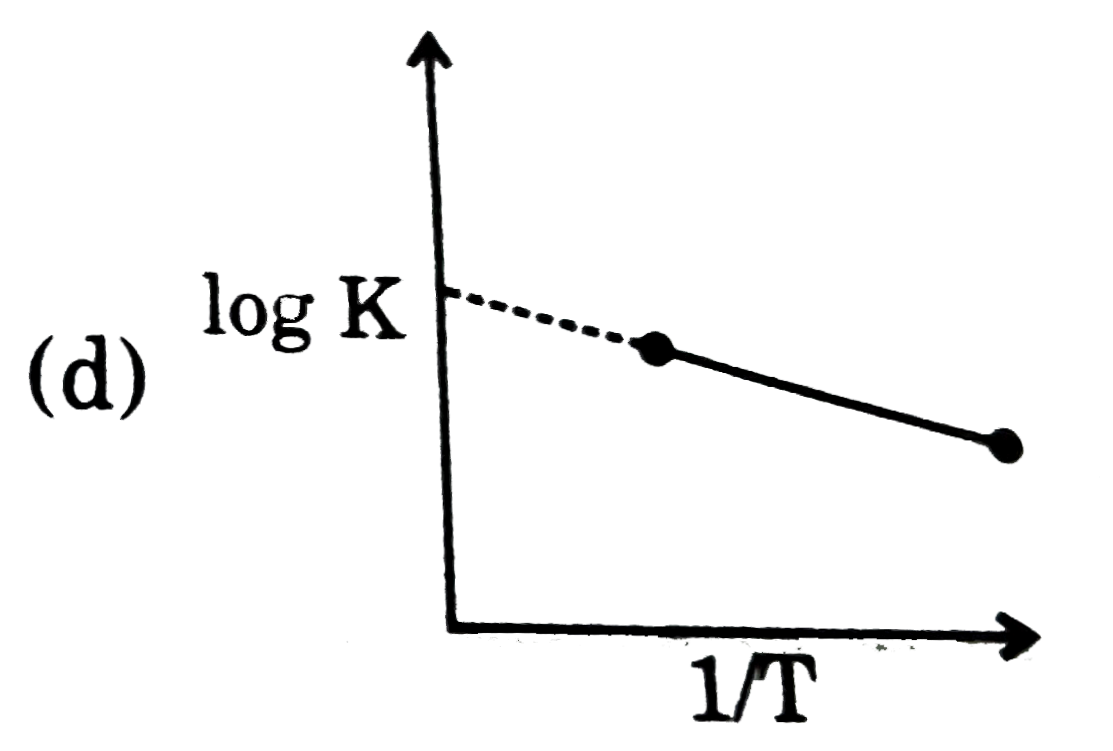
Which one of the following given graphs represents the variation of rate constant (k) with temperature (f) for an endothermic reaction ?
View Solution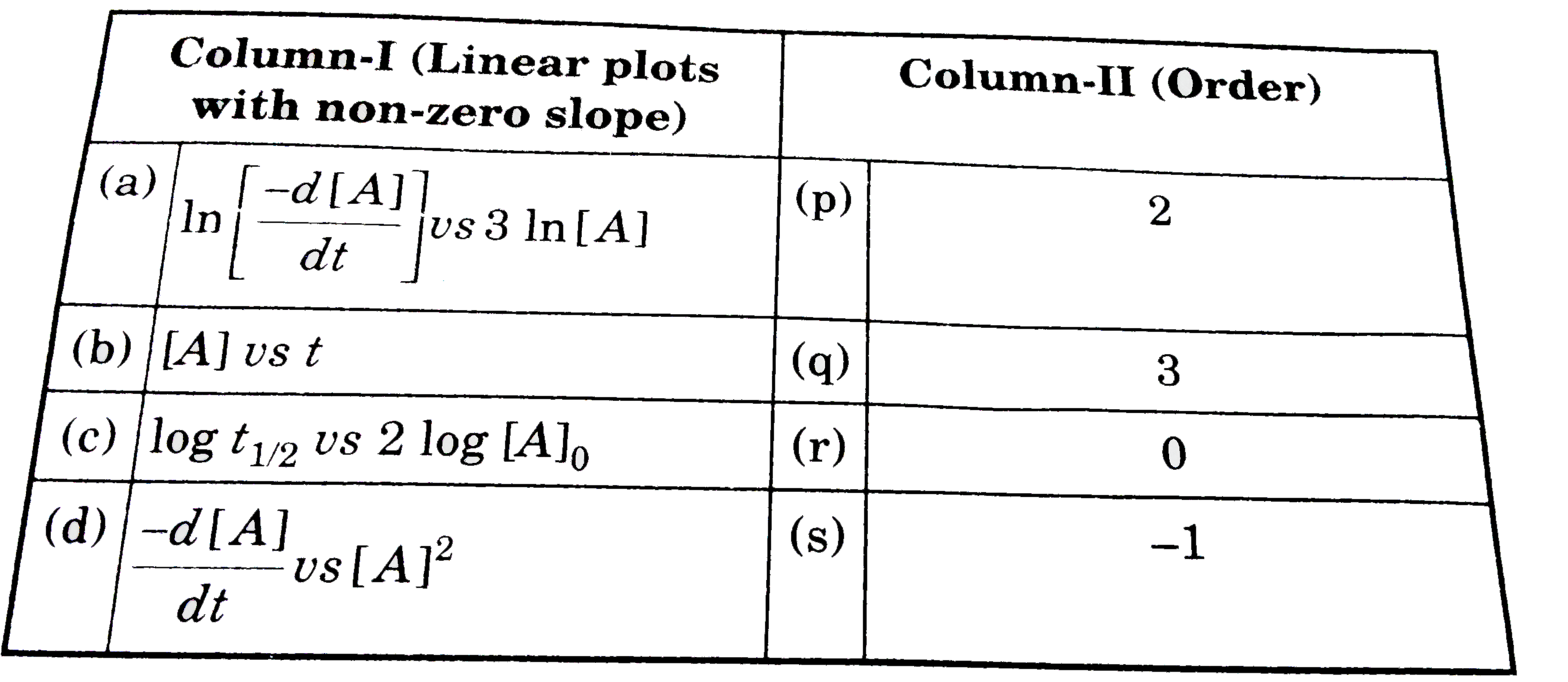
[A] = reactant concentration at time 't', k = rate constant
View SolutionThe rate of a certain reaction increases by 2.5 times when the temperature is raised from 300K at 310K. If k is the rate constant at 300K then the rate constant at 310 K will be equal to
View SolutionThe activation energy of a reaction is zero. Its rate constant at 280 K is 16×10−6s−1 the rate constant at 300k is
View SolutionWhich of the following graphs is incorrect regarding rate constant (k) and absolute temperature ? [Symbols have usual meaning]
View Solution
