If I is the centre of a circle inscribed in a ΔABC, then ∣∣¯¯¯¯¯¯BC∣∣¯¯¯¯¯IA+∣∣¯¯¯¯¯¯CA∣∣¯¯¯¯¯IB+∣∣¯¯¯¯¯¯AB∣∣¯¯¯¯¯IC=Solution in Telugu
¯0
¯¯¯¯¯IA+¯¯¯¯¯IB+¯¯¯¯¯IC
¯¯¯¯¯IA+¯¯¯¯¯IB+¯¯¯¯¯IC3
2(¯¯¯¯¯IA+¯¯¯¯¯IB+¯¯¯¯¯IC)
The correct Answer is:A
Step by step video, text & image solution for If I is the centre of a circle inscribed in a DeltaABC, then abs(bar(BC))bar(IA)+abs(bar(CA))bar(IB)+abs(bar(AB))bar(IC)= by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF VECTORSBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES
55 Videos
- PROPERTIES OF VECTORSBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - EXERCISE - I
31 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL II) (Linked Comprehension Type Questions Passage -III:)
3 Videos
- RATE MEASUREMENTBOOK - AAKASH SERIESCHAPTER - RATE MEASUREMENTEXERCISE - PRACTICE SHEET (EXERCISE - 1) (LEVEL - 1) (STRAIGHT OBJECTIVE TYPE QUESTION)
43 Videos
Similar Questions
If ¯¯¯¯¯¯OA=¯i+2¯j−3¯k,¯¯¯¯¯¯OB=3¯i−2¯j+5¯kand2¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB then ¯¯¯¯¯¯AC=
View SolutionThe position vectors of A and B are ¯aand¯b respectively. If C is a point on the line ¯¯¯¯¯¯AB such that ¯¯¯¯¯¯AC=5¯¯¯¯¯¯AB then find the position vector of C.
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A.
If BC = 6, AC = 8, then the length of side AB is equal to
View SolutionIf a particle moves alonga straight line by S=4t2−8t+3 and the time at which the particle comes of rest is 't' seconds then '2t' is
View SolutionIn DeltaABC, |bar(CB)| = a, |bar(CA)| = b and |bar(AB)| =c. CD is the median through the vertex C. Then bar(CA).bar(CD)=
View SolutionABC is an equilateral triangle of side ‘a'. Then bar(AB).bar(BC) +bar(BC).bar(CA)+ bar(CA).bar(AB) =
View SolutionWhat is the angle between ?
(i) ¯¯¯¯¯¯ABand¯¯¯¯¯¯AC
(ii) ¯¯¯¯¯¯ABand¯¯¯¯¯¯BC
View SolutionProve the following boolean relations. bar(AB + BC + CA) = bar(A)bar(B) + bar(B)bar(C ) +bar(C)bar(A)
View SolutionIf D is the mid -point of side AB of ΔABC, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AC=
View SolutionIf (1, 2), (4, 3), (6, 4) are the midpoints of the sides ¯¯¯¯¯¯BC,¯¯¯¯¯¯CA,¯¯¯¯¯¯AB of ΔABC, then the equation of AB is
View SolutionIn the figure, O is the centre of the circle and AB = CD. OM is perpendicular on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯ON is perpendicular on ¯¯¯¯¯¯CD. Then prove that OM = ON.

View SolutionIn the figure, O is the centre of the circle and AB = CD. OM is perpendicular on bar(AB) and bar(ON) is perpendicular on bar(CD) . Then prove that OM = ON.
View SolutionIn the figure, O is the centre of the circle and AB = CD. OM is perpendicular on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯ON is perpendicular on ¯¯¯¯¯¯CD. Then prove that OM = ON.
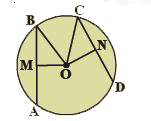
View SolutionIn the figure, O is the centre of the circle and AB = CD. OM is perpendicular on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯ON is perpendicular on ¯¯¯¯¯¯CD. Then prove that OM = ON.
View SolutionIn a right angled triangle ABC, hypotenuse AB=P then ¯¯¯¯¯¯AB.¯¯¯¯¯¯AC+¯¯¯¯¯¯BC.¯¯¯¯¯¯BA+¯¯¯¯¯¯CA.¯¯¯¯¯¯CB = ………
View Solution
