The graph betwee √E and 1p is (E=kinetic energy and p= momentum)




The correct Answer is:C
P=√2mE it is clear that P∝√E
So the graph between P and √E will be straight line. But graph between 1P and √E will be hyperbola
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - WORK , ENERGY , POWER AND COLLISIONEXERCISE - Assertion & Reason For AIIMS Aspirants30videos
WORK , ENERGY , POWER AND COLLISION
- BOOK - ERRORLESS CHAPTER - WORK , ENERGY , POWER AND COLLISIONEXERCISE - Self Evaluation Test19videos
WORK , ENERGY , POWER AND COLLISION
- BOOK - ERRORLESS CHAPTER - WORK , ENERGY , POWER AND COLLISIONEXERCISE - Critical Thinking (Objective Questions)20videos
WORK , ENERGY , POWER AND COLLISION
- BOOK - ERRORLESS CHAPTER - WAVES AND SOUNDEXERCISE - SET25videos
WAVES AND SOUND
- BOOK - ERRORLESS CHAPTER - WORK, ENERGY, POWER & COLLISIONEXERCISE - Assertion30videos
WORK, ENERGY, POWER & COLLISION
Similar Questions
(a) A proton is moving at a speed much less than the speed of light. It has kinetic energy K1 and momentum p1. If the momentum of the proton is doubled, so p2=2p1, how is its new kinetic energy K2 related to K−1?
(b)A photon with energy E1 has momentum p1 . if another photon has momentum p2 that is twice p1, how is the energy E2 of the second photon related to E1?View SolutionRelation between kinetic energy and momentum
Let us consider a body of mass 'm' having a velocity 'v', then
momentum of the body P = mass × velocity
P=m×v⇒v=Pm ...(1)
From definition, kinetic energy (K.E) of the body
K.E=12mv2 ...(2)
Now putting the value of (1) in (2) we have
K.E=12m(Pm)2
K.E.=12mP2m2=12P2m=P22m ...(3)
Thus we can write
P2=2m×K.E
⇒P=√2m×K.E
Thus momentum = √2×mass×kinetic energy
What will be the momentum of a body of mass 100 g having kinetic energy of 20 J ?View Solution
Knowledge Check
- Question 1 - Select One
The graph between linear monentum (p) and Kinetic energy (k) is best represented by
A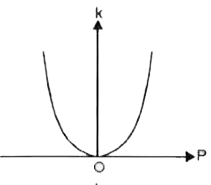 B
B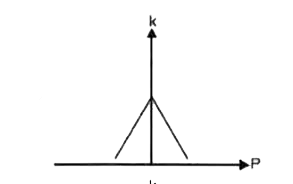 C
C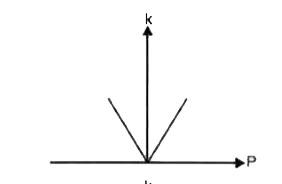 D
D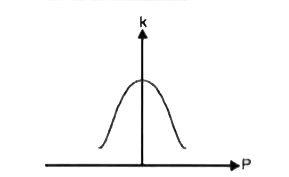
- Question 2 - Select One
The relation between kinetic energy K and linear momentum p of a particle is represented by
AK2=2mpB2K2=mpCp2=2mkD2mK=p - Question 3 - Select One
The relation between kinetic energy K and linear momentum p of a particle is represented by
AK2=2mpB2K2=mpCp2=2mKD2mK=p
The momentum of a body is p and its kinetic energy is E. Its momentum becomes 2p. Its kinetic energy will be
View SolutionAn electron with speed v and a photon with speed c have the same de-Broglic wavelength. If the kinetic energy and momentum of electron is Ee and Pe and that of photon is Eph and Pph respectively, then correct statement is -
View SolutionThe curve between loge L and loge P is (L is the angular momentum and P is the linear momentum).
View SolutionWhich of the following graphs represents the graphical relation between momentum (p) and kinetic energy (K) for a body in motion?
View SolutionWhich one of the following correctly represents the variation between linear momentum (P) and kinetic energy (E) ofa body?
View Solution

