The potential energy of a particle varies with distance x as shown in the graph.
The force acting on the particle is zero at
C
B
B and C
A and D
The correct Answer is:C
it it is clear that slope of U – x curve is zero at point B and C. for point B and C
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - WORK , ENERGY , POWER AND COLLISIONEXERCISE - Assertion & Reason For AIIMS Aspirants30videos
WORK , ENERGY , POWER AND COLLISION
- BOOK - ERRORLESS CHAPTER - WORK , ENERGY , POWER AND COLLISIONEXERCISE - Self Evaluation Test19videos
WORK , ENERGY , POWER AND COLLISION
- BOOK - ERRORLESS CHAPTER - WORK , ENERGY , POWER AND COLLISIONEXERCISE - Critical Thinking (Objective Questions)20videos
WORK , ENERGY , POWER AND COLLISION
- BOOK - ERRORLESS CHAPTER - WAVES AND SOUNDEXERCISE - SET25videos
WAVES AND SOUND
- BOOK - ERRORLESS CHAPTER - WORK, ENERGY, POWER & COLLISIONEXERCISE - Assertion30videos
WORK, ENERGY, POWER & COLLISION
Similar Questions
Knowledge Check
- Question 1 - Select One
The potential energy of a partical veries with distance x as shown in the graph.
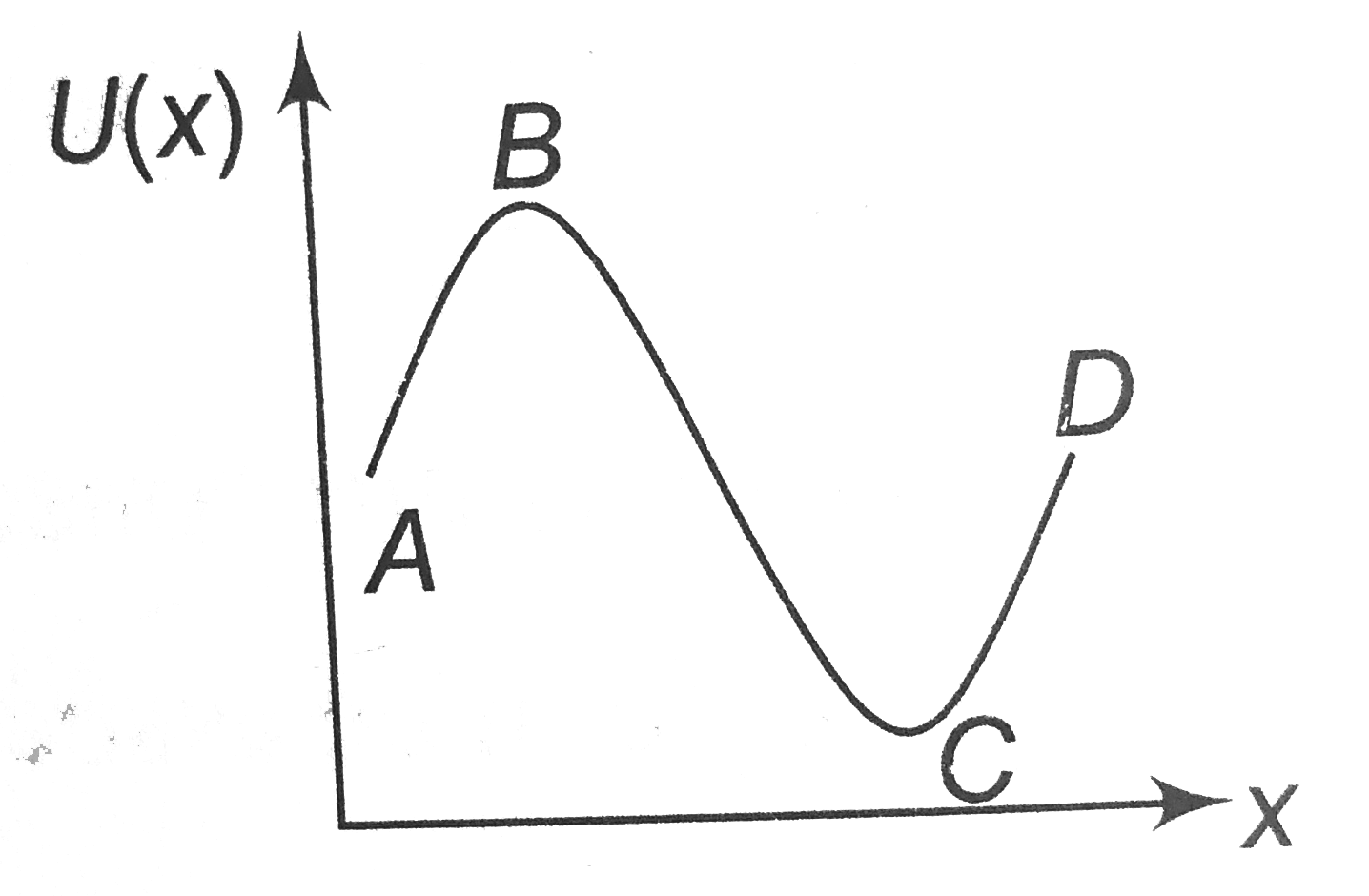
The force acting on the partical is zero atACBBCB and CDA and D - Question 2 - Select One
A force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
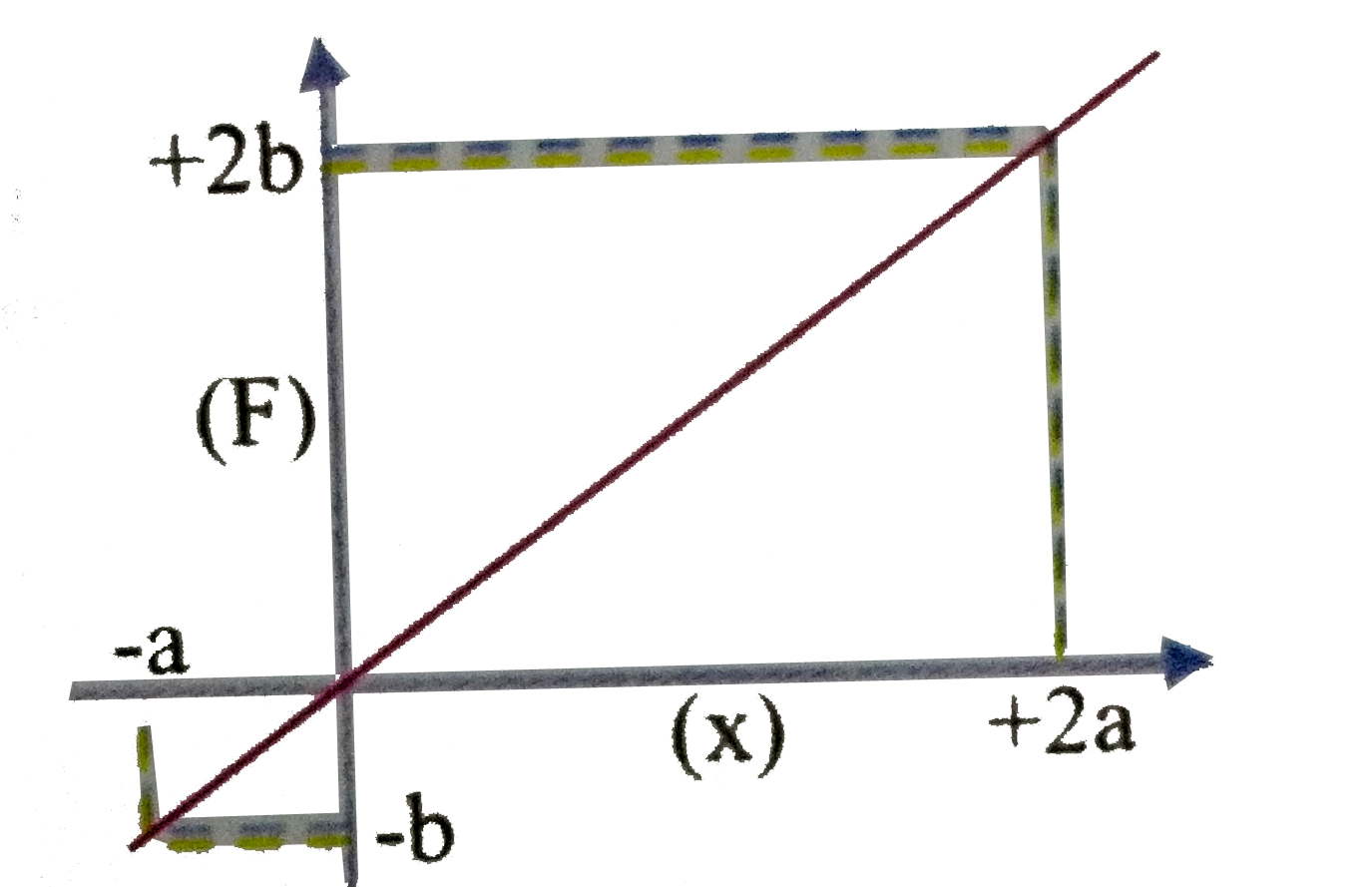.A3ab2B4ab2C23abD24ab - Question 3 - Select One
The displacement time curve of a particle is shown in the figure. The external force acting on the particle is :
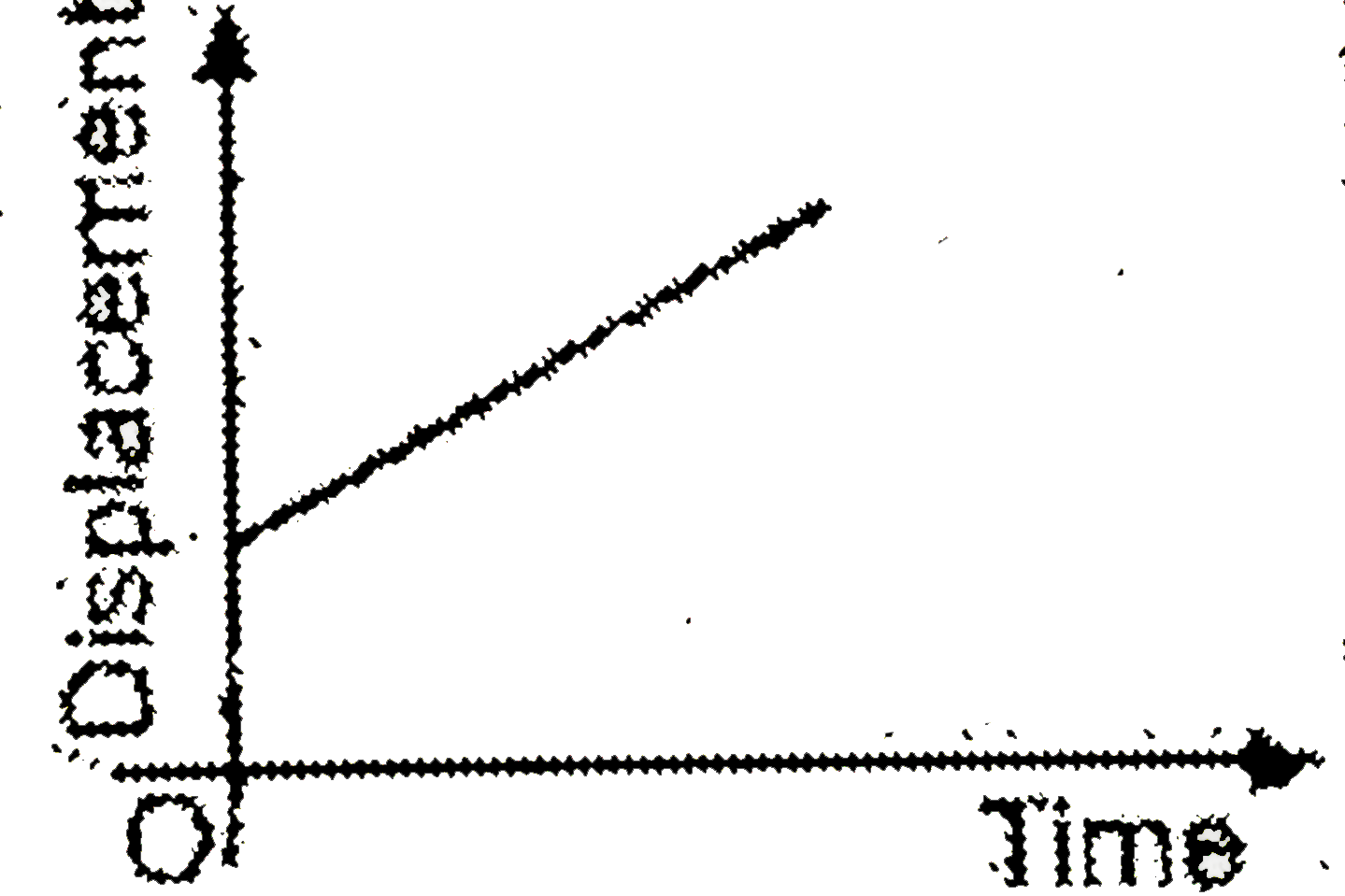AActing at the beginning part of motionBZeroCNot zeroDNone of these
Force acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
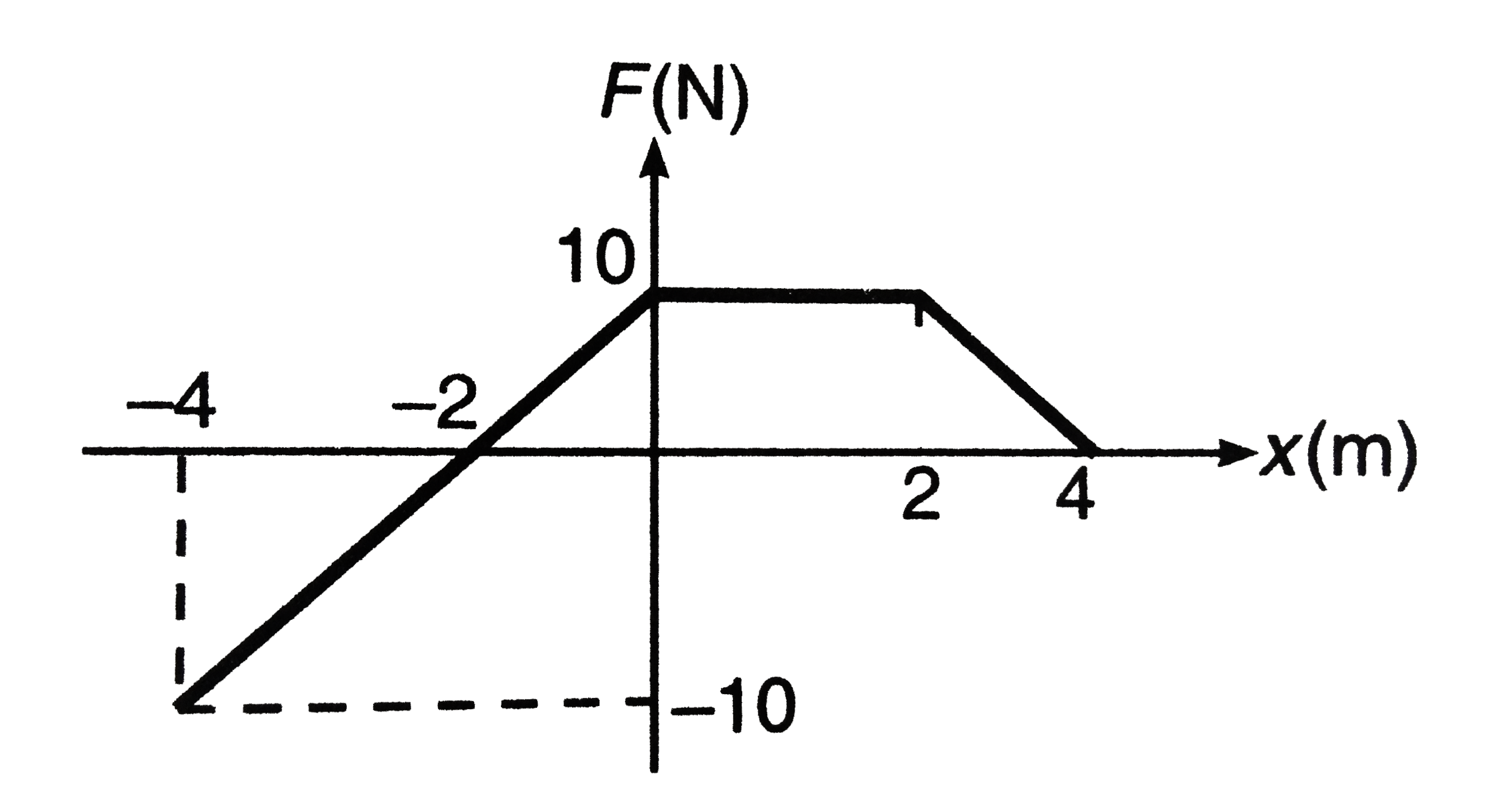. View SolutionKinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionKinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionThe kinetic energy K of a particle moving in a straight line depends on the distances as K=as2. The force acting on the particle is
(where a is a constant)View SolutionThe kinetic energy K of a particle moving along x axis varies with its position (x) as shown in the figure. The magnitude of force acting on particle at x = 9 m is -
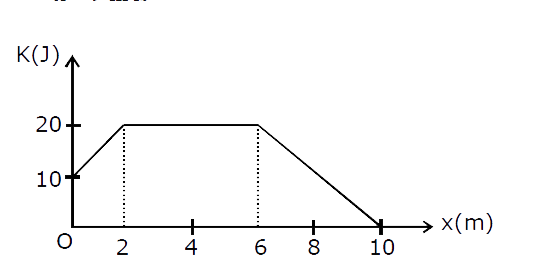View Solution