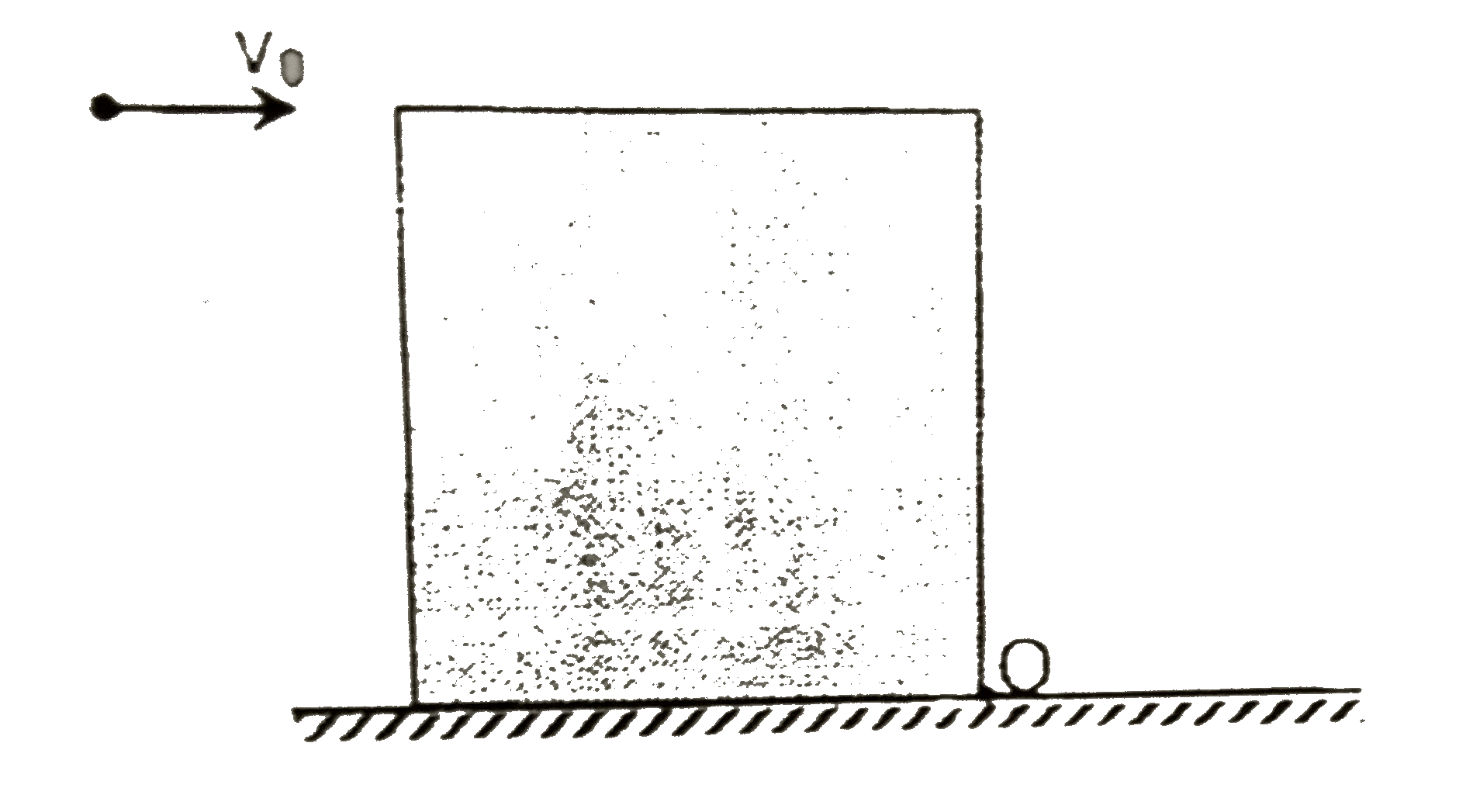
An ice cube of mass M and side of length a each is sliding friction across a counter top with a speed V0 when it hits a ridge O at the edge of the counter (see figure). This collision causes the cube to tilt as shown. The minimum value of V0 needed for the cube to fall of the table is given by V0=√(x+0.1)ag where 'x' is

The correct Answer is:1
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Straight Objective Type Questions
37 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) More than One correct answer Type Questions
15 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Matrix Matching Type Questions
3 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
A cube of mass m and side a is moving along a plane with constant speed vo as shown in figure. The magnitude of angular momentum of the cube about z -axis would be.
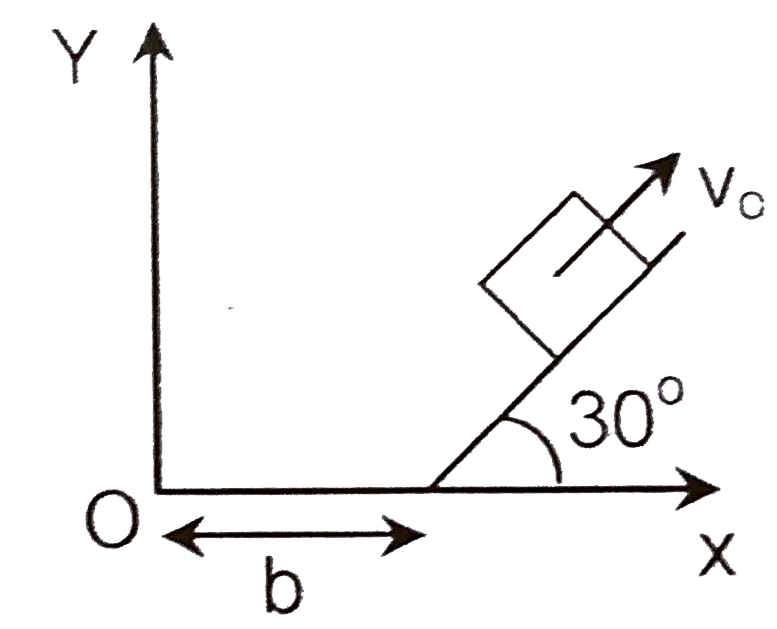
View SolutionA uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
View Solution
Knowledge Check
A cube of mass m and side a is moving along a plane with constant speed vo as shown in figure. The magnitude of angular momentum of the cube about z -axis would be.
 Amvob2B√3mvob2Cmvo(b−a2)DNone of these
Amvob2B√3mvob2Cmvo(b−a2)DNone of theseA solid cube of side 2a and mass M, sliding on a smooth surface with velocity v0 , collides inelastically with the raised edge of the table:
 AMoment of inertia of cube about edge is 4Ma23BMoment of inertia of cube about edge is 8Ma23CMinimum value of v so that cube falls off the table is √1.19gDEnergy of system is conserved
AMoment of inertia of cube about edge is 4Ma23BMoment of inertia of cube about edge is 8Ma23CMinimum value of v so that cube falls off the table is √1.19gDEnergy of system is conservedA uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
ADuring motion , NgtmgBDuring motion, normal reactions acts on the center of massCduring motion, the normal reaction shifts towards positive x-axis from the center of massDduring motion, normal reaction shifts in the direction of the force of friction.
A disc of mass m is moving with constant speed v0 on a smooth horizontal table. Another disc of mass M is placed on the table at rest as shown in the figure. If the collision is elastic, find the velocity of the disc after collision. Both disc lie on the same horizontal plane of the table.

View SolutionIn the adjacent figure, a uniform cube of mass m and edge l=2m is lying at rest an a rough horizontal surface. A small ball of mass m hits the cbe at its top edge with horizontal speed v0 and sticks to it. Friction is so large that the cube can rotate about the edge 'O' without sliding. Calculate the minimum value of v0 ( in m/s) so that the cube will topple. Ignore any loss of energy due to friction at the edge O and take √2−1=0.4.
View SolutionIn the adjacent figure, a uniform cube of mass m and edge l=2m is lying at rest an a rough horizontal surface. A small ball of mass m hits the cbe at its top edge with horizontal speed v0 and sticks to it. Friction is so large that the cube can rotate about the edge 'O' without sliding. Calculate the minimum value of v0 ( in m/s) so that the cube will topple. Ignore any loss of energy due to friction at the edge O and take √2−1=0.4.

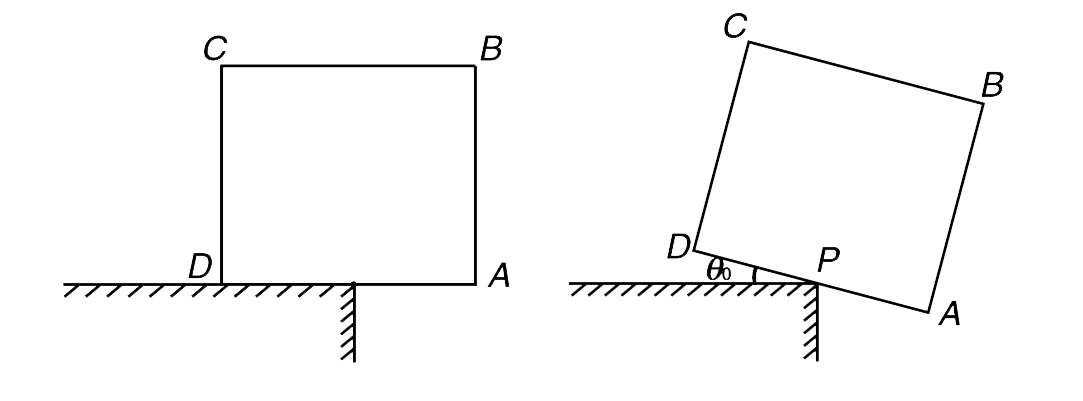
View SolutionA uniform cube of mass M and side length a is placed at rest at the edge of a table. With half of the cube overhanging from the table, the cube begins to roll off the edge. There is sufficient friction at the edge so that the cube does not slip at the edge of the table. Find -
(a) the angle θ0 through which the cube rotates before it leaves contact with the table.
(b) the speed of the centre of the cube at the instant it breaks off the table.
(c) the rotational kinetic energy of the cube at the instant its face AB becomes horizontal.
View SolutionA disk slides across a smooth, level tabletop at height H at a constant speed v0. It slides off the edge of the table and hits the floor a distance x away as shown in the figure.

What is the relationship between the distances x and H?
View Solution
