Four particles, each of mass m, are lying symmetrically on the rim of a disc of mass M and radius R. M.I. of this system about an axis passing through one of the particles and perpendicular to plane of disc is
15MR22
17MR2
19MR22
29MR22
Step by step video & image solution for Four particles, each of mass m, are lying symmetrically on the rim of a disc of mass M and radius R. M.I. of this system about an axis passing through one of the particles and perpendicular to plane of disc is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Calculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionFour similar point masses (each of mass m) are placed on the circumference of a disc of mass M and radius R. The M.I. of the system about the normal axis through the centre O will be:
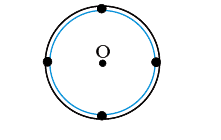
View Solution
Knowledge Check
Four particles each of mass m are lying symmetrically on the rim of a disc of mass M and radius R. Moment of inertia of this system about an axis passing through one of the particles and I to plane of disc is
A16mR2B(3M+16m)R22C(3m+12M)R22DzeroFour similar point masses (m each) are symmetrically placed on the circumference of a disc of mass M and radius R. Moment of inertia of the system about an axis passing through centre O and perpendicular to the plane of the disc will be
AMR2+4mR2BMR2+85mR2CmR2+4MR2DMR22+4mR2The M.I. of disc of mass M and radius 'R' about an axis passing through midway between centre and circumference and perpendicular to its plane is
AMR2/2B5/4MR2CMR2D3/4MR2
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionThe moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
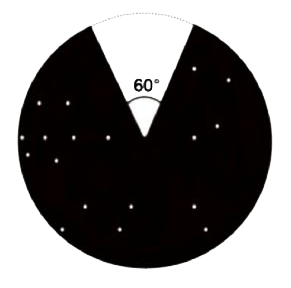
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View Solution