Four concentric conducting spherical shells P, Q, R and S of radii a, 2a, 3a and 4a respectively. Shell P and S are given charges q and −q respectively. If shell R is grounded then potential difference (VP — VR) is (where V, and VR are potential at surfaces of P and R respectively)
q12πε0a
q6πε0a
q24πε0a
q16πε0a
To solve the problem, we need to find the potential difference VP−VR between the surfaces of the spherical shells P and R, given that shell P has charge q, shell S has charge −q, and shell R is grounded.
1. Identify the Charges on the Shells:
- Shell P (radius a) has charge q.
- Shell S (radius 4a) has charge −q.
- The charges on the other shells can be determined by the properties of conductors:
- Shell Q (radius 2a) will have charge 0 because it is between P and S.
- Shell R (radius 3a) will have a charge Q′ that we need to find.
2. Determine Charge on Shell R:
- Since shell R is grounded, its potential must be zero.
- The charge Q′ on shell R can be calculated using the formula for grounded conductors:
Q′=−q4⋅3a4a=−3q16
- This means shell R has a net charge of −3q16.
3. Calculate the Potential at Shell P (VP):
- The potential VP at the surface of shell P is given by the contributions from all other shells:
VP=k(qa−q2a+0−3q/163a)
- Simplifying this:
VP=k(qa−q2a−q16a)
- Finding a common denominator (16a):
VP=k(16q−8q−q16a)=k(7q16a)
4. Calculate the Potential at Shell R (VR):
- Since shell R is grounded, its potential VR=0.
5. Calculate the Potential Difference VP−VR:
- Now we can find the potential difference:
VP−VR=VP−0=k(7q16a)
6. Final Result:
- The potential difference VP−VR is:
VP−VR=7kq16a
- Shell P (radius a) has charge q.
- Shell S (radius 4a) has charge −q.
- The charges on the other shells can be determined by the properties of conductors:
- Shell Q (radius 2a) will have charge 0 because it is between P and S.
- Shell R (radius 3a) will have a charge Q′ that we need to find.
- Since shell R is grounded, its potential must be zero.
- The charge Q′ on shell R can be calculated using the formula for grounded conductors:
Q′=−q4⋅3a4a=−3q16
- This means shell R has a net charge of −3q16.
- The potential VP at the surface of shell P is given by the contributions from all other shells:
VP=k(qa−q2a+0−3q/163a)
- Simplifying this:
VP=k(qa−q2a−q16a)
- Finding a common denominator (16a):
VP=k(16q−8q−q16a)=k(7q16a)
- Since shell R is grounded, its potential VR=0.
- Now we can find the potential difference:
VP−VR=VP−0=k(7q16a)
- The potential difference VP−VR is:
VP−VR=7kq16a
Topper's Solved these Questions
Similar Questions
Figure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.

View SolutionFigure shows three concentric thin conducting spherical shells A, B and C of radii R, 2R and 3R. The shell B is earthed A and C are given charges q and 2q respectively. Find the charges appearing on all the surface of A,B and C.

[inner surface (A)0,(B)−q,(C)43q
Outer surface (A)q,(B)−43q,(C)23q]
View Solution
Knowledge Check
There are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
AKq2aBkKq3aCKq4aDkq6aThere are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
Akq2aBkq4aCkq3aDkq6aA current of 2 A flows in an electric circuit as shown in figure. The potential difference (VR−VS), in volts (VR and VS are potentials at R and S respectively is
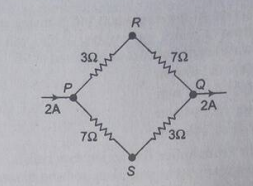 A-4B(+2)C(+4)D-2
A-4B(+2)C(+4)D-2
There are two concentric conducting spherical shells of radius rA and rB respectively (rB=2rA). If the inner shell is given a charge Q and outer shell is given a charge 2Q, then the potential difference between the surfaces of the shells will be K=14πε0
View SolutionA current of 2 A flows in an electric circuit as shown in figure. The potential difference (VR−VS), in volts (VR and VS are potentials at R and S respectively is

View SolutionTwo uniformly charged concentric spherical shells of radius R and r, are given charges Q1 and Q2 respectively. If their potential difference is V, then it will not depends upon:

View Solution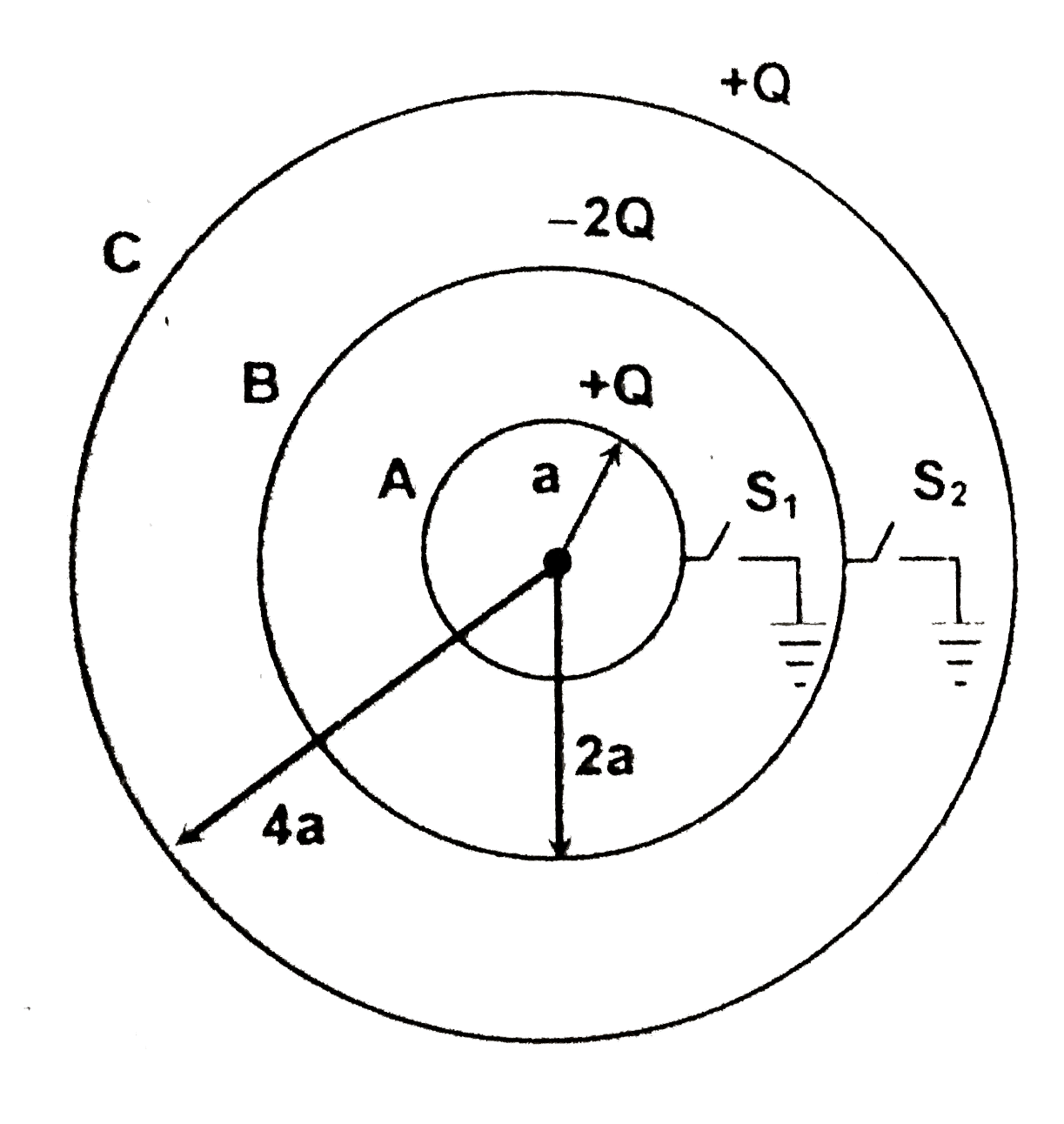
Three concentric spherical conducting shells A, B and C of radii a, 2a and 4a are initially given charges +Q, -2Q and +Q respectively. The charge on the middle spherical shell B after switches S1 and S2 are simultaneously closed, will be
View SolutionThere are four concentric spherical shells A, B, C and D of radii R, 2R, 3R and 4R respectively. Net charge on all the spherical shells are same and equal to Q. If VA,VB,VC)andVD represent electric potentials of A, B, C and D respectively, the magnitude of VD=V.

View Solution
