A resistance of 2Ω is connected across one gap of a meter bridge (the length of the wire is 100cm and an unknown resistance, greater than 2Ω, is connected across the other gap. When these resistance are interchanged, the balance point shifts by 20cm. Neglecting any corrections, the unknown resistance is.
(a)3Ω
(b) 4Ω
( c) 5Ω
(d) 6Ω.
The correct Answer is:A
To solve the problem, we will use the principles of a meter bridge and the concept of balancing lengths. Here’s a step-by-step solution:
Step 1: Understand the setup
We have a meter bridge with one gap occupied by a known resistance R1=2Ω and the other gap occupied by an unknown resistance Rx which is greater than 2Ω. The total length of the meter bridge is 100cm.
Step 2: Establish the first balance condition
When the bridge is balanced, the ratio of the resistances is equal to the ratio of the lengths:
RxR1=L100−L
Substituting R1=2Ω:
Rx2=L100−L(1)
Step 3: Establish the second balance condition after interchanging resistances
When the resistances are interchanged, the balance point shifts by 20cm. The new balance point is L+20cm. The new balance condition is:
R1Rx=L+20100−(L+20)=L+2080−L(2)
Step 4: Set up the equations
From equation (1):
Rx=2⋅L100−L
From equation (2):
2Rx=L+2080−L
This can be rearranged to:
Rx=2⋅80−LL+20
Step 5: Equate the two expressions for Rx
Now we have two expressions for Rx:
1. Rx=2⋅L100−L
2. Rx=2⋅80−LL+20
Setting them equal to each other:
2⋅L100−L=2⋅80−LL+20
Step 6: Simplify the equation
Cancel 2 from both sides:
L100−L=80−LL+20
Cross-multiplying gives:
L(L+20)=(100−L)(80−L)
Step 7: Expand and simplify
Expanding both sides:
L2+20L=8000−100L+80L+L2
L2+20L=8000−20L+L2
Cancelling L2 from both sides:
20L+20L=8000
40L=8000
L=200cm
Step 8: Substitute L back to find Rx
Using L=40cm in equation (1):
Rx=2⋅40100−40=2⋅4060=2⋅23=43Ω
Step 9: Check the options
The unknown resistance Rx is 3Ω.
Final Answer
The unknown resistance is 3Ω.
We have a meter bridge with one gap occupied by a known resistance R1=2Ω and the other gap occupied by an unknown resistance Rx which is greater than 2Ω. The total length of the meter bridge is 100cm.
When the bridge is balanced, the ratio of the resistances is equal to the ratio of the lengths:
RxR1=L100−L
Substituting R1=2Ω:
Rx2=L100−L(1)
When the resistances are interchanged, the balance point shifts by 20cm. The new balance point is L+20cm. The new balance condition is:
R1Rx=L+20100−(L+20)=L+2080−L(2)
From equation (1):
Rx=2⋅L100−L
From equation (2):
2Rx=L+2080−L
This can be rearranged to:
Rx=2⋅80−LL+20
Now we have two expressions for Rx:
1. Rx=2⋅L100−L
2. Rx=2⋅80−LL+20
2⋅L100−L=2⋅80−LL+20
Cancel 2 from both sides:
L100−L=80−LL+20
L(L+20)=(100−L)(80−L)
Expanding both sides:
L2+20L=8000−100L+80L+L2
L2+20L=8000−20L+L2
Cancelling L2 from both sides:
20L+20L=8000
40L=8000
L=200cm
Using L=40cm in equation (1):
Rx=2⋅40100−40=2⋅4060=2⋅23=43Ω
The unknown resistance Rx is 3Ω.
The unknown resistance is 3Ω.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.83videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Single Correct33videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.63videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery49videos
FLUID MECHANICS
Similar Questions
A resistance of 2Ω is connected across one gap of a meter bridge (the length of the wire is 100cm) and an unknown resistance, greater than 2Ωis conneted across the other gap. When these resistances are interchanged, the balance point shifts by 20cm. Neglecting any corrections,the unknown resistance is
View SolutionResistance in the two gaps of a meter bridge are 10ohm and 30ohm respectively. If the resistances are interchanged he balance point shifts by
View Solution
Knowledge Check
- Question 1 - Select One
Two resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
A3B6C9D12
Find the current through the 10Ω resistance connected across AB
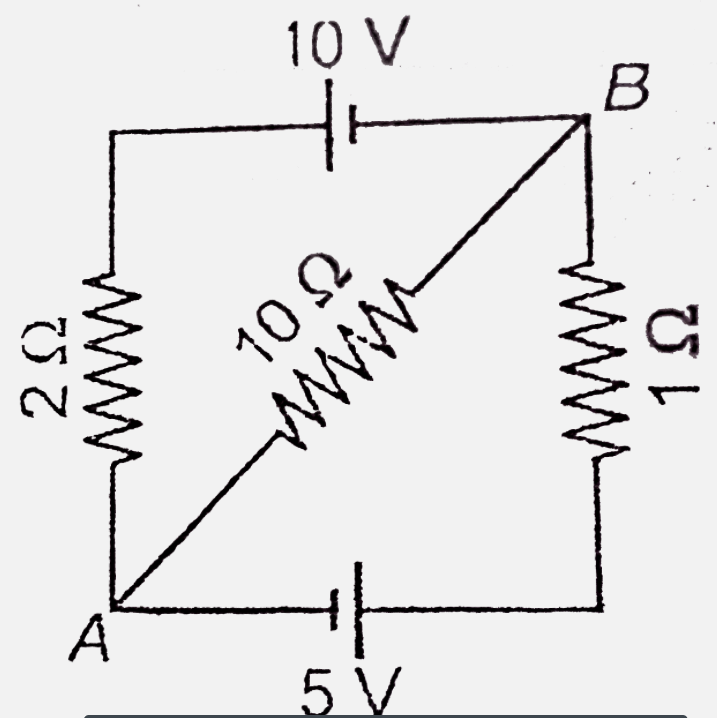 View Solution
View SolutionTwo resistances are connected in two gaps of a meter bridge. The balance point is 20cm from the zero end. A resistance of 15Ω is connected in series with the smaller of the two. The null point shifts to 40cm. The value of the smaller resistance in Ω is
View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View SolutionTwo unknown resistances are connected in two gaps of a meter-bridge. The null point is obtained at 40 cm from left end. A 30Ω resistance is connected in series with the smaller of the two resistances, the null point shifts by 20 cm to the right end. The value of smaller resistance in Ω is
View SolutionThe resistance of each arm of the wheat stone bridge is 10Ω. A resistance of 10Ω is connected in series with galvanometer then the equivalent resistance across the battery will be:-
View SolutionIn a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
View Solution

