A solid disk is rolling without slipping on a level surface at a constant speed of . How far can it roll up a ramp before it stops? (take
To solve the problem of how far a solid disk can roll up a 30-degree ramp before it stops, we will use the principle of conservation of energy. Here's a step-by-step solution:
Step 1: Understand the Energy Conservation Principle
The total mechanical energy of the disk will be conserved as it rolls up the ramp. Initially, the disk has kinetic energy (both translational and rotational) and no potential energy. As it rolls up the ramp, this kinetic energy is converted into potential energy until it comes to a stop.
Step 2: Write the Energy Equations
1. Initial Kinetic Energy (KE_initial):
The total kinetic energy of the disk can be expressed as:
KEinitial=KEtranslational+KErotational=12mv2+12Iω2
For a solid disk, the moment of inertia I is given by:
I=12mr2
The angular velocity ω can be related to the linear velocity v by:
ω=vr
Therefore, substituting ω:
KEinitial=12mv2+12(12mr2)(v2r2)=12mv2+14mv2=34mv2
2. Potential Energy (PE_final):
When the disk reaches height h, its potential energy is given by:
PEfinal=mgh
Step 3: Set the Initial Kinetic Energy Equal to Final Potential Energy
Using the conservation of energy:
34mv2=mgh
We can cancel m from both sides (assuming m≠0):
34v2=gh
Step 4: Solve for Height h
Rearranging the equation gives:
h=3v24g
Substituting the values v=2m/s and g=9.8m/s2:
h=3×(2)24×9.8=1239.2≈0.306m
Step 5: Relate Height to Distance Along the Ramp
Using the geometry of the ramp, we can relate the height h to the distance d along the ramp using the sine of the angle:
sin(30∘)=hd
Since sin(30∘)=12:
12=hd⟹d=2h
Substituting h:
d=2×0.306≈0.612m
Final Answer
The disk can roll approximately 0.612 meters up the ramp before it stops.
---
The total mechanical energy of the disk will be conserved as it rolls up the ramp. Initially, the disk has kinetic energy (both translational and rotational) and no potential energy. As it rolls up the ramp, this kinetic energy is converted into potential energy until it comes to a stop.
1. Initial Kinetic Energy (KE_initial):
The total kinetic energy of the disk can be expressed as:
KEinitial=KEtranslational+KErotational=12mv2+12Iω2
For a solid disk, the moment of inertia I is given by:
I=12mr2
The angular velocity ω can be related to the linear velocity v by:
ω=vr
Therefore, substituting ω:
KEinitial=12mv2+12(12mr2)(v2r2)=12mv2+14mv2=34mv2
When the disk reaches height h, its potential energy is given by:
PEfinal=mgh
Using the conservation of energy:
34mv2=mgh
We can cancel m from both sides (assuming m≠0):
34v2=gh
Rearranging the equation gives:
h=3v24g
Substituting the values v=2m/s and g=9.8m/s2:
h=3×(2)24×9.8=1239.2≈0.306m
Using the geometry of the ramp, we can relate the height h to the distance d along the ramp using the sine of the angle:
sin(30∘)=hd
Since sin(30∘)=12:
12=hd⟹d=2h
Substituting h:
d=2×0.306≈0.612m
The disk can roll approximately 0.612 meters up the ramp before it stops.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 21videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A solid sphere is rolling without slipping on a level surface dat a constant speed of 2.0ms−1 How far can it roll up a 30∘ ramp before it stops ?
View SolutionA uniform sphere of mass 200 g rolls without slipping on a plane surface so that its centre moves at a speed of 2.00 cm/s. Find its kinetic energy.
View SolutionA uniform sphere of mass 500g rolls without slipping on a plane surface so that its centre moves at a speed of 0.02m/s.
The total kinetic energy of rolling sphere would be (in J)View SolutionA unifrom sphere of mass 500 g rolls without slipping on a plants horizontal surface with its center moving at a speed of 5.00cm/s .It kinetic energy is :
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
View SolutionA uniform ring rolls down an inclined plane without slipping. If it reaches the bottom of a speed of 2m/s, then calculate the height of the inclined plane (use g=10m/s2)
View SolutionA uniform ring rolls down an inclined plane without slipping. If it reaches the bottom of a speed of 2m/s, then calculate the height of the inclined plane (use g=10m/s2)
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA cylinder is rolling without slipping on a plank which is also moving with speed 10m/s on a horizontal surface as shown. The speed of centre of the cylinder is 20m/s. The mass of cylinder is 2kg. The kinetic energy of the cylinder when observed from ground is
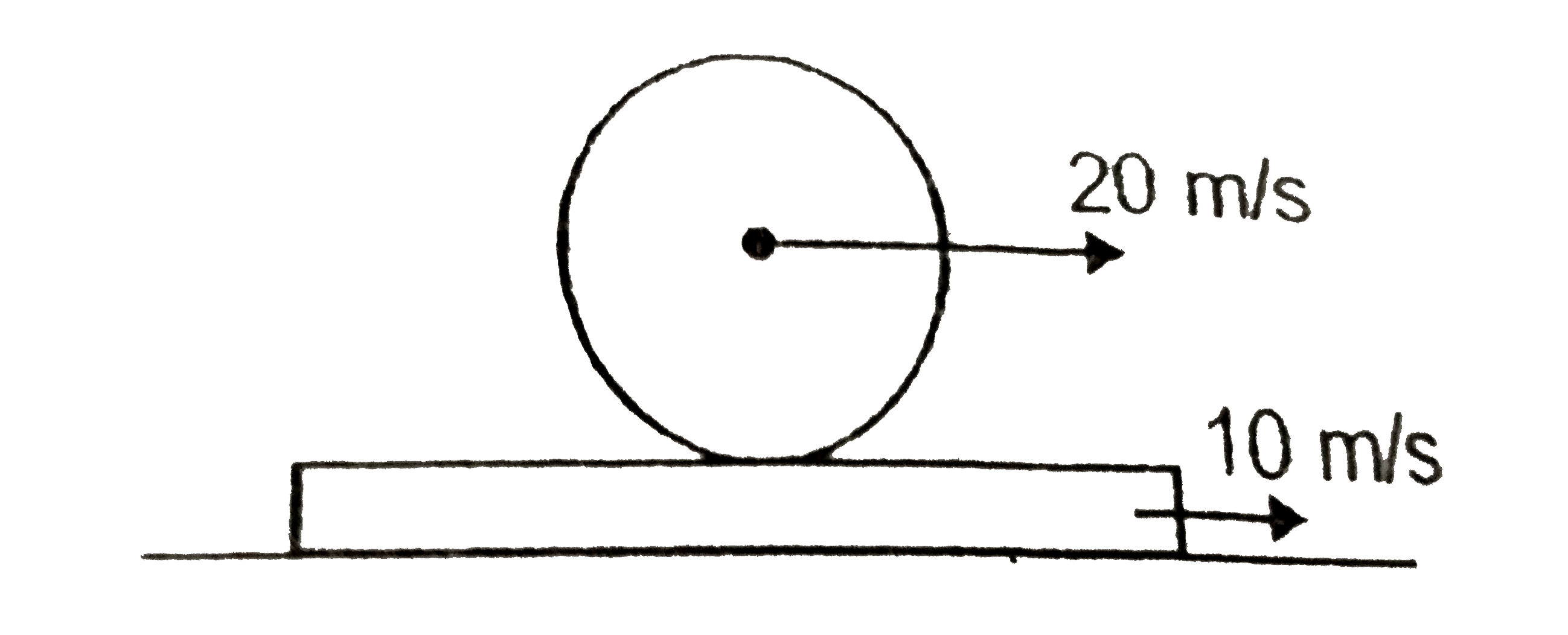 View Solution
View Solution

