Four point masses each of mass m are placed on vertices of a regular tetrahedron. Distance between any two masses is r.
Gravitation field at centre at zero
Gravitation potential at centre is −4Gmr
Gravitation potential energy of system in −6Gm2r
Gravitation force on one of the point mass is √6Gm2r2
The correct Answer is:A, C, D
To solve the problem of finding the gravitational potential energy and the net force acting on the point masses at the vertices of a regular tetrahedron, we can follow these steps:
1. Understanding the Configuration:
We have four point masses, each of mass m, placed at the vertices of a regular tetrahedron. The distance between any two masses is given as r.
2. Gravitational Potential Energy Calculation:
The gravitational potential energy U of a system of point masses is given by the formula:
U=−Gm1m2r12−Gm1m3r13−Gm1m4r14−Gm2m3r23−Gm2m4r24−Gm3m4r34
In our case, since all masses are equal and the distance between any two masses is r, we can simplify this:
U=−6Gm2r
Here, there are 6 pairs of masses, each contributing −Gm2r to the potential energy.
3. Calculating the Gravitational Force Between Two Masses:
The gravitational force F between any two point masses is given by:
F=Gm2r2
4. Finding the Net Force on One Mass:
Each mass experiences gravitational attraction from the other three masses. The angle between the forces exerted by any two masses on a third mass is 60∘ due to the geometry of the tetrahedron.
The net force →Fnet can be calculated using vector addition. The magnitude of the net force can be found using the formula:
F2net=F21+F22+F23+2F1F2cos(60∘)+2F2F3cos(60∘)+2F3F1cos(60∘)
Since F1=F2=F3=F:
F2net=3F2+3F2⋅12=3F2+32F2=62F2=3F2
Thus,
Fnet=√3F=√3(Gm2r2)
Final Results:
- The gravitational potential energy of the system is:
U=−6Gm2r
- The net force acting on one mass due to the other three is:
Fnet=√3Gm2r2
We have four point masses, each of mass m, placed at the vertices of a regular tetrahedron. The distance between any two masses is given as r.
The gravitational potential energy U of a system of point masses is given by the formula:
U=−Gm1m2r12−Gm1m3r13−Gm1m4r14−Gm2m3r23−Gm2m4r24−Gm3m4r34
In our case, since all masses are equal and the distance between any two masses is r, we can simplify this:
U=−6Gm2r
Here, there are 6 pairs of masses, each contributing −Gm2r to the potential energy.
The gravitational force F between any two point masses is given by:
F=Gm2r2
Each mass experiences gravitational attraction from the other three masses. The angle between the forces exerted by any two masses on a third mass is 60∘ due to the geometry of the tetrahedron.
F2net=F21+F22+F23+2F1F2cos(60∘)+2F2F3cos(60∘)+2F3F1cos(60∘)
Since F1=F2=F3=F:
F2net=3F2+3F2⋅12=3F2+32F2=62F2=3F2
Thus,
Fnet=√3F=√3(Gm2r2)
- The gravitational potential energy of the system is:
U=−6Gm2r
- The net force acting on one mass due to the other three is:
Fnet=√3Gm2r2
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4020videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.419videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.3820videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
Four point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
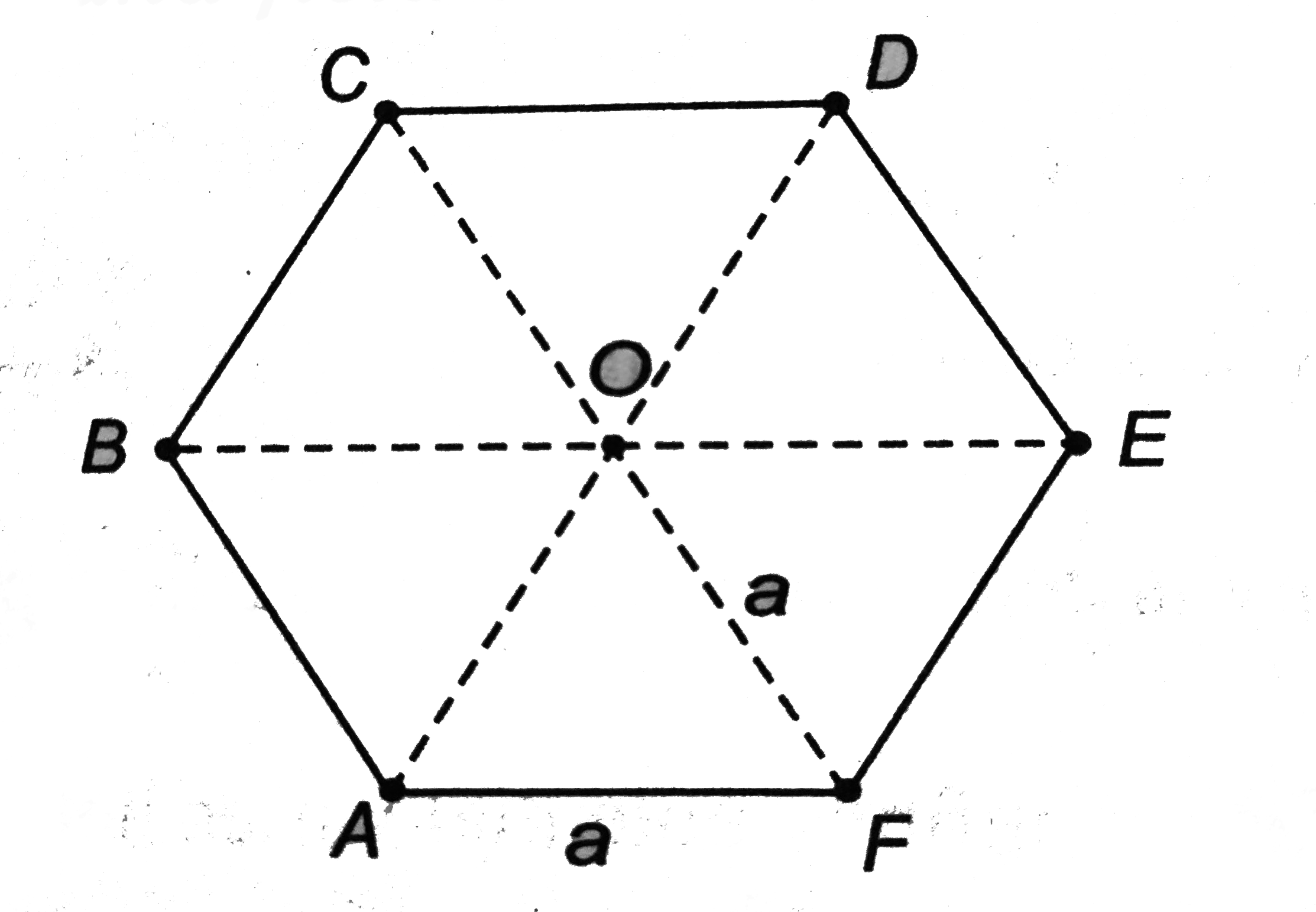 .View Solution
.View SolutionFive point masses m each are kept at five vertices of a regular pentagon. Distance of center of pentagon from any one of the vertice is 'a'. Find gravitational potential and filed strength at center.
View Solution
Knowledge Check
- Question 1 - Select One
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
AGm2l2[54+1√3]BGm2l2[34+1√3]CGm2l2[54−1√3]DGm2l2[34−1√3] - Question 2 - Select One
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−√2Gm2l(2−1√2)B−2Gm2l(2+1√2)C−√2Gm2l(√2−1√2)D−2Gm2l(√2−1√2)
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
View SolutionAssertion : Four point masses each of mass m are placed at points 1, 2, 3 and 6 of a regular hexagon of side a. Then the gravitational field at the centre of hexagon is Gma2
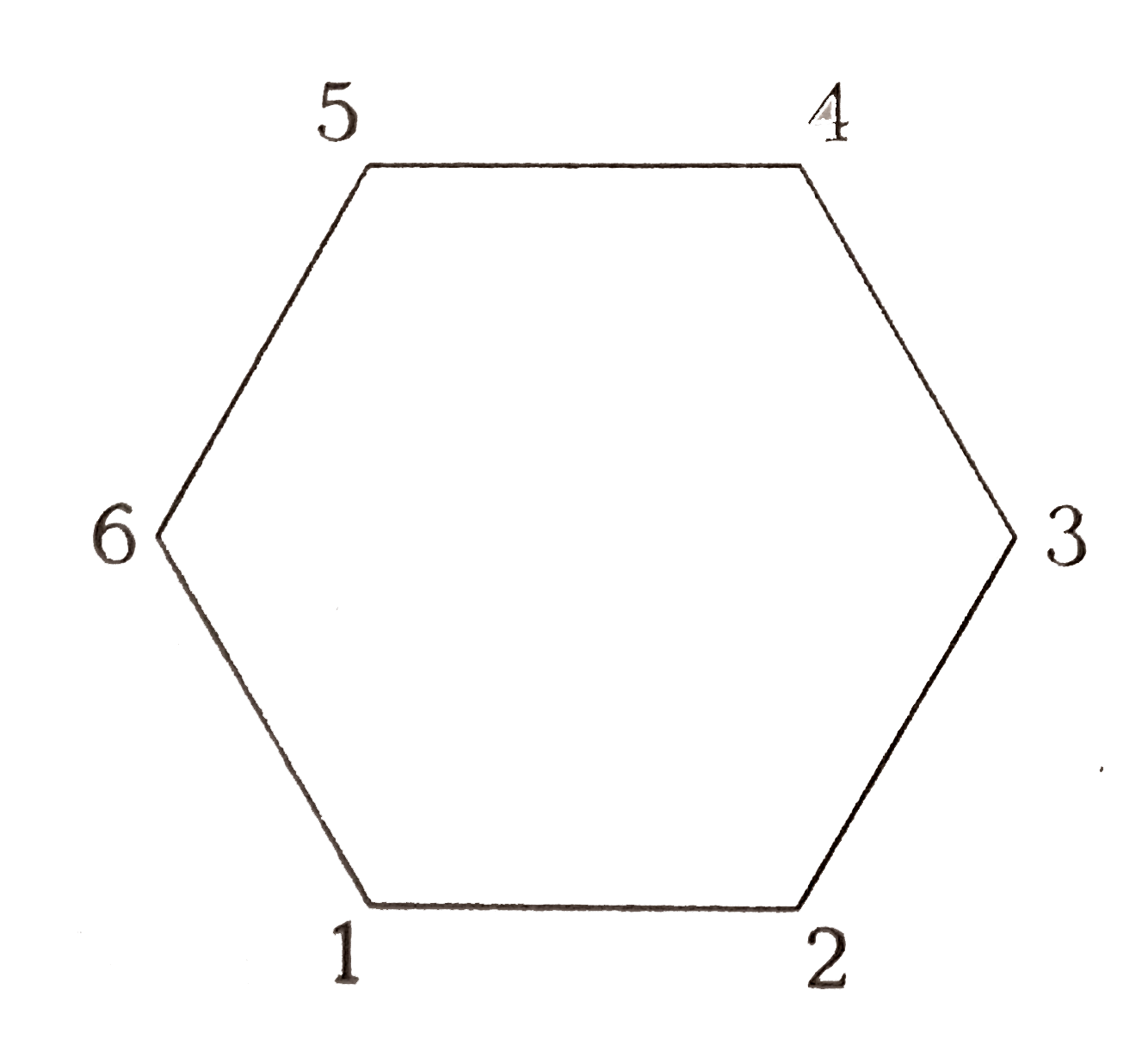
Reason : The field strength due to masses at 3 and 6 are cancelled out.View SolutionFour small point charges (each of equal magnitude q) are placed at four corners of a regular tetrahedron of side a. find out potential energy of charge system
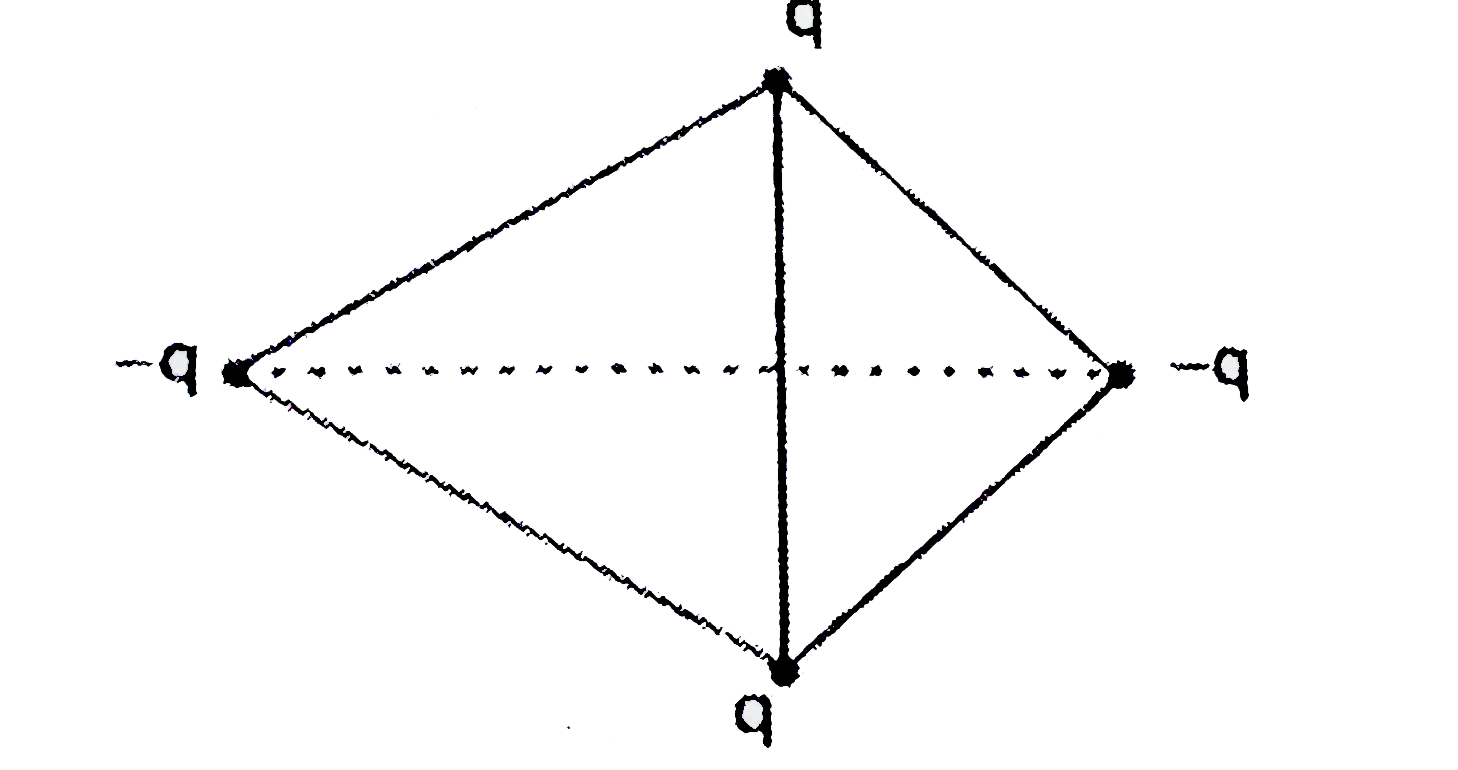 View Solution
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral triangle of side 1. What is the gravitational field and potential due to the three masses at the centroid of the triangle ?
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?
View Solution

