Current passing through a wire decreases linearly from 10A to 0 in 4s. Find total charge flowing through the wire in the given time interval.
To solve the problem of finding the total charge flowing through a wire when the current decreases linearly from 10 A to 0 A in 4 seconds, we can follow these steps:
1. Understand the relationship between current and charge:
The current (I) is defined as the rate of flow of charge (Q) with respect to time (t). Mathematically, this is expressed as:
I=dQdt
Rearranging this gives us:
dQ=Idt
2. Identify the nature of the current change:
The current decreases linearly from 10 A to 0 A over a time interval of 4 seconds. This means we can represent the current as a function of time.
3. Graph the current vs. time:
We can visualize the current as a triangle on a graph where:
- The x-axis represents time (0 to 4 seconds).
- The y-axis represents current (from 10 A to 0 A).
The graph will form a right triangle with:
- Base = 4 seconds (time interval)
- Height = 10 A (initial current)
4. Calculate the area of the triangle:
The area of the triangle represents the total charge (Q) that has flowed through the wire. The area (A) of a triangle is given by the formula:
A=12×base×height
Substituting the known values:
A=12×4s×10A
5. Perform the calculation:
A=12×4×10=20Coulombs
6. Conclusion:
The total charge flowing through the wire in the given time interval is:
Q=20C
Final Answer:
The total charge flowing through the wire is 20 Coulombs.
The current (I) is defined as the rate of flow of charge (Q) with respect to time (t). Mathematically, this is expressed as:
I=dQdt
Rearranging this gives us:
dQ=Idt
The current decreases linearly from 10 A to 0 A over a time interval of 4 seconds. This means we can represent the current as a function of time.
We can visualize the current as a triangle on a graph where:
- The x-axis represents time (0 to 4 seconds).
- The y-axis represents current (from 10 A to 0 A).
The graph will form a right triangle with:
- Base = 4 seconds (time interval)
- Height = 10 A (initial current)
The area of the triangle represents the total charge (Q) that has flowed through the wire. The area (A) of a triangle is given by the formula:
A=12×base×height
Substituting the known values:
A=12×4s×10A
A=12×4×10=20Coulombs
The total charge flowing through the wire in the given time interval is:
Q=20C
The total charge flowing through the wire is 20 Coulombs.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Example Type 1
Explore 2 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Example Type 2
Explore 1 Video
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrances gallery
Explore 25 Videos
Similar Questions
A constant current of 4A passes through a wire for 8s. Find total charge flowing through that wire in the given time interval.
View SolutionCurrent through a wire decreases from 4 A to zero in 10sec. Calculate charge flown through the wire during this interval of time.
View SolutionThe current flowing through wire depends on time as, I=3t2+2t+5
The charge flowing through the cross - section of the wire in time t=0 to t=2 second is
View SolutionThe current through a wire depends on time as, i=(10+4t) Here , i is ampere and t in seconds. Find the charge crossed through section in time interval between t=0 to t=10s.
View SolutionThe plot represents the flow of current through a wire at three different times. The ratio of charges flowing through the wire at different time is
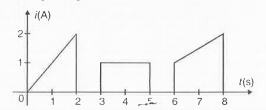
View SolutionThe plot represents the flow of current through a wire at three different times. The ratio of charges flowing through the wire at diffferent times is

View SolutionThe current through a wire depends on time as
I=i0+αt,
where i0=10Aandα=4As−1.Find the charge crossed through a section of the wire in 10 second
View SolutionIf charge flown through a wire is given by q=3sin(3t), then
Q. Find out the current flown through the wire at t=π9 second.
View SolutionIf charge flown through a wire is given by q=3sin(3t), then
Q. Find out the amount of charge flown through the wire at t=(π6) seconds.
View SolutionIf charge flown through a wire is given by q=3sin(3t), then
Q. Find out the amount of charge flown through the wire at t=(π6) seconds.
View Solution
