An - particle is the nucleus of a helium atom. It has a mas kg and as charge c. compare the force of the electric repulsion between two -particles with the force of gravitational attraction between them.
The correct Answer is:A, C
To solve the problem of comparing the electric repulsion force between two alpha particles with the gravitational attraction force between them, we can follow these steps:
Step 1: Calculate the Electric Force of Repulsion (Fe)
The electric force of repulsion between two charges can be calculated using Coulomb's law:
Fe=k⋅q1⋅q2r2
Where:
- k is Coulomb's constant, k=14πϵ0≈9×109N m2/C2
- q1 and q2 are the charges of the alpha particles, which are both +2e (where e≈1.6×10−19C).
- r is the distance between the two particles.
Since both charges are the same, we can simplify this to:
Fe=k⋅q2r2
Substituting q=2e:
Fe=k⋅(2e)2r2=4k⋅e2r2
Step 2: Calculate the Gravitational Force of Attraction (Fg)
The gravitational force between two masses can be calculated using Newton's law of gravitation:
Fg=G⋅m1⋅m2r2
Where:
- G is the gravitational constant, G≈6.67×10−11N m2/kg2
- m1 and m2 are the masses of the alpha particles, which are both m=6.64×10−27kg.
Thus, we can simplify this to:
Fg=G⋅m2r2
Step 3: Find the Ratio of Electric Force to Gravitational Force
Now, we can find the ratio of the electric force to the gravitational force:
FeFg=4k⋅e2r2G⋅m2r2=4k⋅e2G⋅m2
Step 4: Substitute Values
Substituting the known values:
- k≈9×109N m2/C2
- e≈1.6×10−19C
- G≈6.67×10−11N m2/kg2
- m=6.64×10−27kg
Calculating e2:
e2≈(1.6×10−19)2=2.56×10−38C2
Now substituting these values into the ratio:
FeFg=4⋅(9×109)⋅(2.56×10−38)(6.67×10−11)⋅(6.64×10−27)2
Calculating (6.64×10−27)2:
(6.64×10−27)2≈4.40×10−53kg2
Now substituting this back into the ratio:
FeFg=4⋅(9×109)⋅(2.56×10−38)(6.67×10−11)⋅(4.40×10−53)
Step 5: Final Calculation
Calculating the numerator:
4⋅(9×109)⋅(2.56×10−38)≈9.216×10−28
Calculating the denominator:
(6.67×10−11)⋅(4.40×10−53)≈2.9388×10−63
Now dividing:
9.216×10−282.9388×10−63≈3.14×1035
Conclusion
Thus, the ratio of the electric repulsion force to the gravitational attraction force between two alpha particles is approximately:
FeFg≈3.14×1035
The electric force of repulsion between two charges can be calculated using Coulomb's law:
- k is Coulomb's constant, k=14πϵ0≈9×109N m2/C2
- q1 and q2 are the charges of the alpha particles, which are both +2e (where e≈1.6×10−19C).
- r is the distance between the two particles.
The gravitational force between two masses can be calculated using Newton's law of gravitation:
- G is the gravitational constant, G≈6.67×10−11N m2/kg2
- m1 and m2 are the masses of the alpha particles, which are both m=6.64×10−27kg.
Now, we can find the ratio of the electric force to the gravitational force:
Substituting the known values:
- e≈1.6×10−19C
- G≈6.67×10−11N m2/kg2
- m=6.64×10−27kg
Calculating the numerator:
Thus, the ratio of the electric repulsion force to the gravitational attraction force between two alpha particles is approximately:
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective15videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE6videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason19videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
Two spherical balls of mass 10 kg each are placed 100 m apart. Find the gravitational force of attraction between them.
View SolutionTwo spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
View SolutionThe force of attraction between two particles of masses 12 kg ans 25kg is 1.4×10−8N .Calculate the separation between the particles.
View SolutionTwo positively charged small particles, each of mass 1.7×10−27kg and carrying a charge of 1.6×10−19C are placed apart at a separation r. If each one experiences a repulsive force equal to its weight find their separation.
View SolutionTwo point charges q1=2×10−3C and q2=−3×10−6C are separated by a distance x=10 cm. Find the magnitude and nature of the force between the two charges.
View SolutionA proton has a mass 1.67 ×10−27 kg and charge +1.6×10−19C. If the proton is accelerated through a potential difference of million volts, then the kinetic energy is
View SolutionAn α-particle of mass 6.65×10−27kg is travelling at right angles to a magnetic field with a speed of 6×105ms−1. The strength of the magnetic field is 0.2T. Calculate the force on the α-particle and its acceleration.
View SolutionA particle of mass 1kg is kept on the surface of a uniform sphere of mass 20kg and radius 1.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
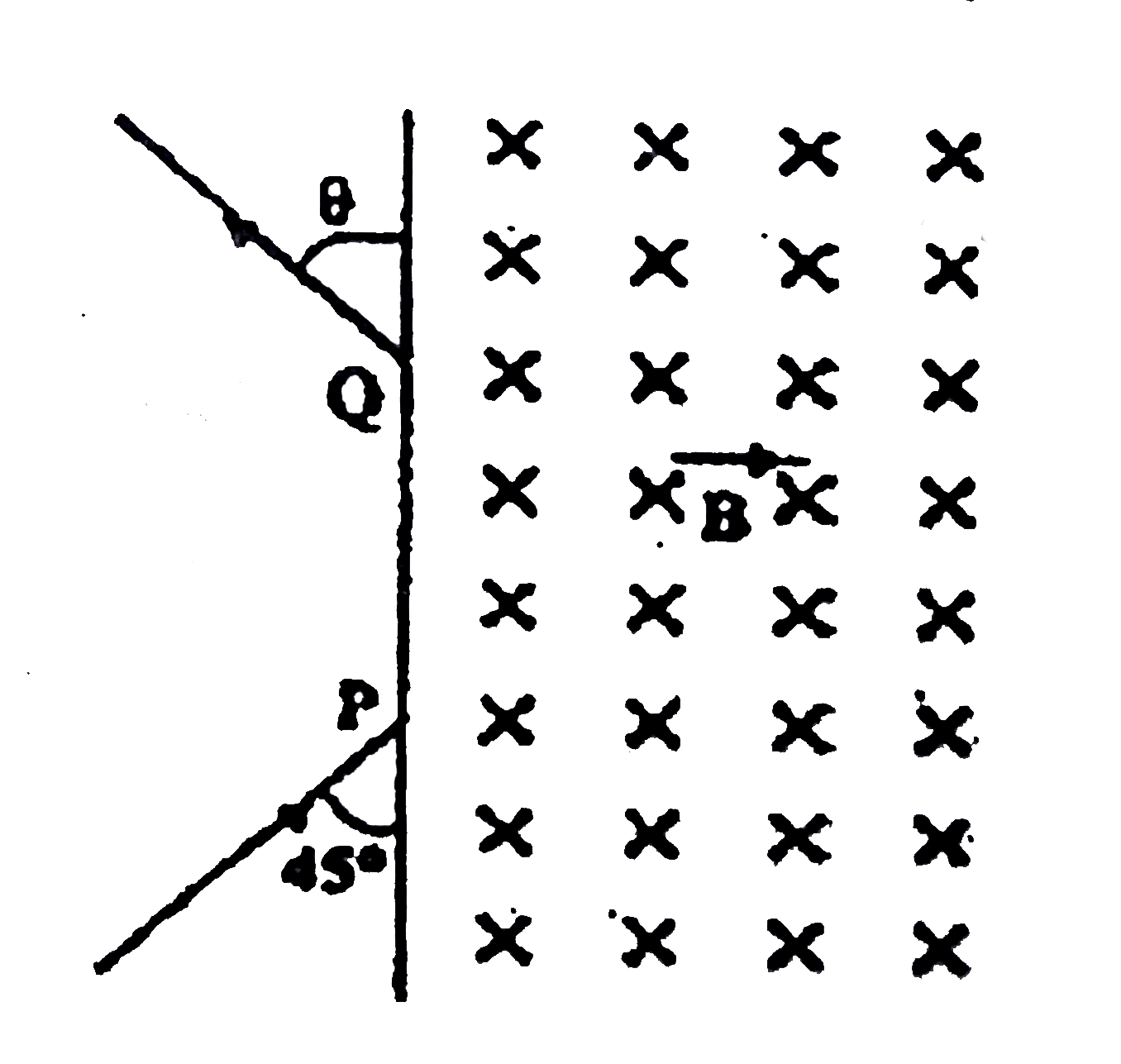 View Solution
View SolutionA particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View Solution

