Three concentric, thin, spherical, metallic shells have radii 1, 2, and 4 cm and they are held at potentials 10,0 and 40V respectively. Taking the origin at the common centre, calculate the following:
(a) Potential at r = 1.25 cm
(b) Potential at r = 2.5 cm
(c) Electric field at r =1.25 cm
The correct Answer is:A, B
To solve the problem, we need to find the potential at specific points and the electric field at a given point for three concentric metallic spherical shells with given radii and potentials.
Given Data:
- Radii of the shells:
- r1=1cm
- r2=2cm
- r3=4cm
- Potentials:
- V1=10V (at r1)
- V2=0V (at r2)
- V3=40V (at r3)
Step 1: Establish the equations for the potentials
The potential V at a distance r from the center due to a spherical shell is given by:
V=k(Q1r1+Q2r2+Q3r3)
where k is the electrostatic constant and Q1,Q2,Q3 are the charges on the shells.
From the given potentials at the shells, we can write three equations:
1. For r=1cm:
k(Q11+Q22+Q34)=10
This simplifies to:
4Q1+2Q2+Q3=40(Equation 1)
2. For r=2cm:
k(Q12+Q22+Q34)=0
This simplifies to:
2Q1+2Q2+Q3=0(Equation 2)
3. For r=4cm:
k(Q14+Q24+Q34)=40
This simplifies to:
Q1+Q2+Q3=160(Equation 3)
Step 2: Solve the equations
Now we need to solve the three equations simultaneously.
From Equation 2:
Q3=−2Q1−2Q2
Substituting Q3 into Equation 1:
4Q1+2Q2−2Q1−2Q2=40
This simplifies to:
2Q1=40⟹Q1=20
Now substituting Q1 back into Equation 2:
2(20)+2Q2+Q3=0⟹40+2Q2+Q3=0
Substituting Q3:
40+2Q2−2(20+Q2)=0⟹40+2Q2−40−2Q2=0
This gives us no new information, so we can use Equation 3:
20+Q2+Q3=160
Substituting Q3:
20+Q2−2(20+Q2)=160
Solving this gives:
20+Q2−40−2Q2=160⟹−Q2=160−20⟹Q2=−180
Finally, substituting Q2 back to find Q3:
Q3=−2(20)−2(−180)=−40+360=320
Summary of Charges:
- Q1=20
- Q2=−180
- Q3=320
Step 3: Calculate the potentials at r=1.25cm and r=2.5cm
(a) Potential at r=1.25cm:
V(1.25)=k(Q11.25+Q22.5+Q34)
Substituting the values:
V(1.25)=k(201.25+−1802.5+3204)
Calculating:
=k(16−72+80)=k⋅24
Assuming k=1 for simplicity, we get:
V(1.25)=6V
(b) Potential at r=2.5cm:
V(2.5)=k(Q12.5+Q22.5+Q34)
Substituting the values:
V(2.5)=k(202.5+−1802.5+3204)
Calculating:
=k(8−72+80)=k⋅16
Assuming k=1 for simplicity, we get:
V(2.5)=16×102V
(c) Electric field at r=1.25cm:
The electric field E inside a conductor is given by:
E=−dVdr
Using the potential derived earlier:
E(1.25)=k(Q1(1.25)2+Q2(2.5)2+Q3(4)2)
Substituting the values:
=k(201.5625+−1806.25+32016)
Calculating:
=k(12.8−28.8+20)=k⋅4
Assuming k=1 for simplicity, we get:
E(1.25)=12.8V/m
Final Answers:
(a) Potential at r=1.25cm = 6 V
(b) Potential at r=2.5cm = 1600 V
(c) Electric field at r=1.25cm = 12.8 V/m
- Radii of the shells:
- r1=1cm
- r2=2cm
- r3=4cm
- Potentials:
- V1=10V (at r1)
- V2=0V (at r2)
- V3=40V (at r3)
The potential V at a distance r from the center due to a spherical shell is given by:
V=k(Q1r1+Q2r2+Q3r3)
where k is the electrostatic constant and Q1,Q2,Q3 are the charges on the shells.
k(Q11+Q22+Q34)=10
This simplifies to:
4Q1+2Q2+Q3=40(Equation 1)
k(Q12+Q22+Q34)=0
This simplifies to:
2Q1+2Q2+Q3=0(Equation 2)
k(Q14+Q24+Q34)=40
This simplifies to:
Q1+Q2+Q3=160(Equation 3)
Now we need to solve the three equations simultaneously.
Q3=−2Q1−2Q2
4Q1+2Q2−2Q1−2Q2=40
This simplifies to:
2Q1=40⟹Q1=20
2(20)+2Q2+Q3=0⟹40+2Q2+Q3=0
Substituting Q3:
40+2Q2−2(20+Q2)=0⟹40+2Q2−40−2Q2=0
This gives us no new information, so we can use Equation 3:
20+Q2+Q3=160
Substituting Q3:
20+Q2−2(20+Q2)=160
Solving this gives:
20+Q2−40−2Q2=160⟹−Q2=160−20⟹Q2=−180
Finally, substituting Q2 back to find Q3:
Q3=−2(20)−2(−180)=−40+360=320
- Q1=20
- Q2=−180
- Q3=320
V(1.25)=k(Q11.25+Q22.5+Q34)
Substituting the values:
V(1.25)=k(201.25+−1802.5+3204)
Calculating:
=k(16−72+80)=k⋅24
Assuming k=1 for simplicity, we get:
V(1.25)=6V
V(2.5)=k(Q12.5+Q22.5+Q34)
Substituting the values:
V(2.5)=k(202.5+−1802.5+3204)
Calculating:
=k(8−72+80)=k⋅16
Assuming k=1 for simplicity, we get:
V(2.5)=16×102V
The electric field E inside a conductor is given by:
E=−dVdr
Using the potential derived earlier:
E(1.25)=k(Q1(1.25)2+Q2(2.5)2+Q3(4)2)
Substituting the values:
=k(201.5625+−1806.25+32016)
Calculating:
=k(12.8−28.8+20)=k⋅4
Assuming k=1 for simplicity, we get:
E(1.25)=12.8V/m
(a) Potential at r=1.25cm = 6 V
(b) Potential at r=2.5cm = 1600 V
(c) Electric field at r=1.25cm = 12.8 V/m
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.1
10 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.2
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Two concentric shells have masses M and m and their radii are R and r, respectively, where R>r. What is the gravitational potential at their common centre?
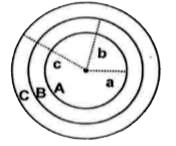
View SolutionThree concentric charged metallic spherical shells A, B and C have radii a,b and c, charge densities σ,−σ and σ and potentials VA,VB and VC respectively. Then which of the following relations is correct?
View Solution
Knowledge Check
Three concentric spherical shells have radii a,b and c(a<b<c) and have surface charge densities σ,−sigam and σ respectively. If VA,VB and VC denote the potentials of the three shells, then for c=a+b, we have
AVC=VB=VABVC=VA≠VBCVC=VB≠VADVC≠VB≠VA
There are two concentric conducting spherical shells of radii 10cm and 20cm. The outer shell is charged to a potential of 50esu while inner shell is earthed. The charge on outer shell is
View SolutionThree concentric conducting spherical shells of radii R, R2 and 3R carry charges Q,-2Q and 3Q, respectively compute the electric field at r=52R

View SolutionThree concentric metallic spherical shells A,B and C of radii a,b and c(a<b<c) have surface charge densities +σ,−σand +σ respectively ,the potential of shell B is
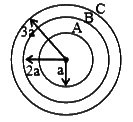
View SolutionThree concentric spherical shells A, B and C having uniformly distributed total charges +Q, -2Q and +Q respectively are placed as shown. The potential at the centre will be -
View SolutionThree concentric metallic spherical shell A,B and C or radii a,b and c(a<b<c) have surface charge densities −σ,+σand−σ. Respectively. The potential of shel A is :
View SolutionThree concentric spherical shells have radii a,b and c(a<b<c) and have surface charge densities σ,−σ and σ respectively. If VA,VB and VC denote the potentials of the three shells, then for c=q+b, we have
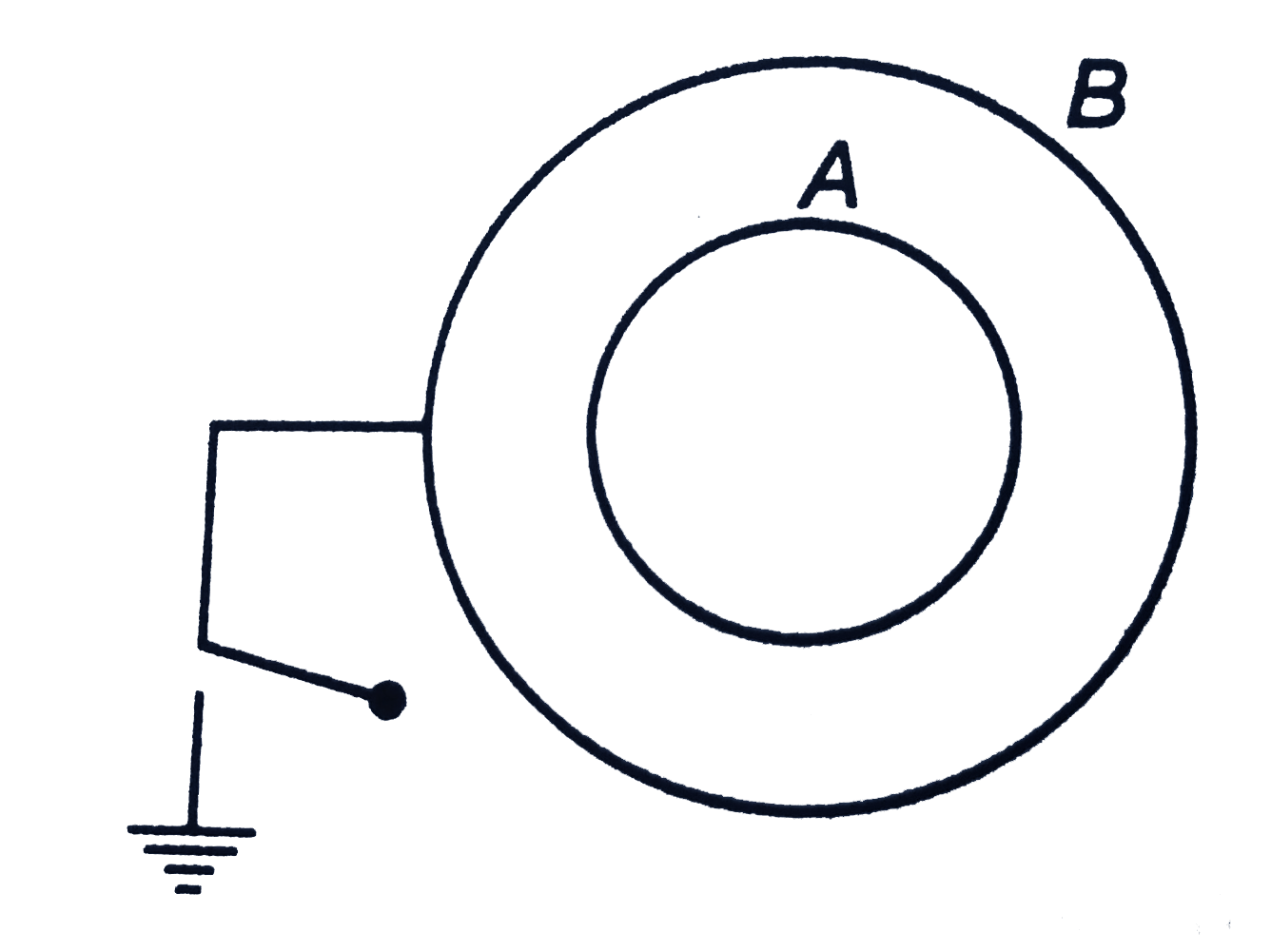
View SolutionTwo concentric shells have radii R and 2R charges qA and qB and potentials 2V and (32)V respectively. Now, shell B is earthed and let charges on them become qA' and qB'. Then,
View Solution
