If the plates of a capacitor are joined together by as conducting wire, then its capacitance
reamains unchanged
decreases
become zero
becomes infinite
The correct Answer is:D
To solve the problem of what happens to the capacitance of a capacitor when its plates are joined together by a conducting wire, we can follow these steps:
Step 1: Understand the Definition of Capacitance
Capacitance (C) is defined as the ability of a system to store charge per unit voltage. Mathematically, it is given by the formula:
C=QV
where:
- C is the capacitance,
- Q is the charge stored on the plates,
- V is the potential difference between the plates.
Step 2: Analyze the Effect of Joining the Plates
When the plates of the capacitor are joined together by a conducting wire, they effectively become a single conductor. This means that the potential difference (V) between the plates becomes zero because both plates are at the same electric potential.
Step 3: Substitute into the Capacitance Formula
Since the potential difference V is now zero, we can substitute this into the capacitance formula:
C=Q0
This expression implies that capacitance approaches infinity because dividing by zero is undefined in mathematics.
Step 4: Conclusion
Thus, when the plates of a capacitor are joined together by a conducting wire, the capacitance approaches infinity. This is because the distance between the plates effectively becomes zero, allowing for an infinite amount of charge to be stored for any finite voltage.
Final Answer
The capacitance of the capacitor approaches infinity.
---
Capacitance (C) is defined as the ability of a system to store charge per unit voltage. Mathematically, it is given by the formula:
C=QV
where:
- C is the capacitance,
- Q is the charge stored on the plates,
- V is the potential difference between the plates.
When the plates of the capacitor are joined together by a conducting wire, they effectively become a single conductor. This means that the potential difference (V) between the plates becomes zero because both plates are at the same electric potential.
Since the potential difference V is now zero, we can substitute this into the capacitance formula:
C=Q0
This expression implies that capacitance approaches infinity because dividing by zero is undefined in mathematics.
Thus, when the plates of a capacitor are joined together by a conducting wire, the capacitance approaches infinity. This is because the distance between the plates effectively becomes zero, allowing for an infinite amount of charge to be stored for any finite voltage.
The capacitance of the capacitor approaches infinity.
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
Knowledge Check
Assertion: The distance between the parallel plates of a capacitor is halved, then its capacitance is doubled.
Reason: The capacitance depends on the introduced dielectric.AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.Assertion: Increasing the charge on the plates of a capacitor means increasing the capacitance.
Resion : Capacitance is directly proportinal to charge.AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.A copper plate of thickness b is placed inside a parallel plate capacitor of plate distance d and area A as shown in figure. The capacitance of capacitor is
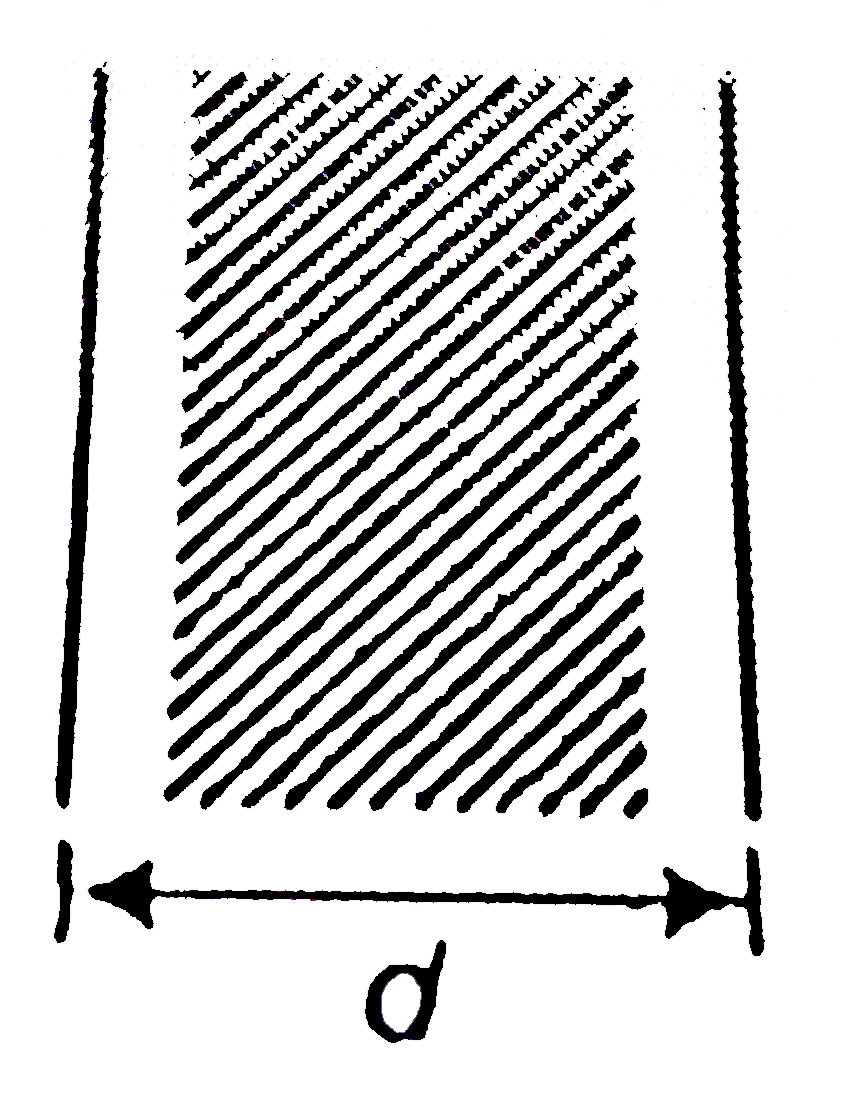 Aε0Ad+b2Bε0A2dCε0Ad−bD2ε0Ad+b2
Aε0Ad+b2Bε0A2dCε0Ad−bD2ε0Ad+b2
A parallel plate capacitor of capacitance C has been charged, so that the potential difference between its plates is V. Now, the plates of this capacitor are connected to another uncharged capacitor of capacitance 2C. Find the common potential acquired by the system and loss of energy.
View SolutionA capacitor having capacity of 2μF is charged to 200V and then the plates of the capacitor are connected to a resistance wire. The heat produced in joule will be
View SolutionA very thin plate of metal is placed exactly in the middle of the two plates of a parallel plate capacitor. What will be the effect on the capacitance of the system?
View SolutionTwo capacitors of capacitance 2μFand5μF are charged to a potential difference 100V and 50 V respectively and connected such that the positive plate of one capacitor is connected to the negative plate of the other capacitor after the switch is closed, the initial current in the circuit is 50 mA. the total resistance of the connecting wires is (in Ohm):
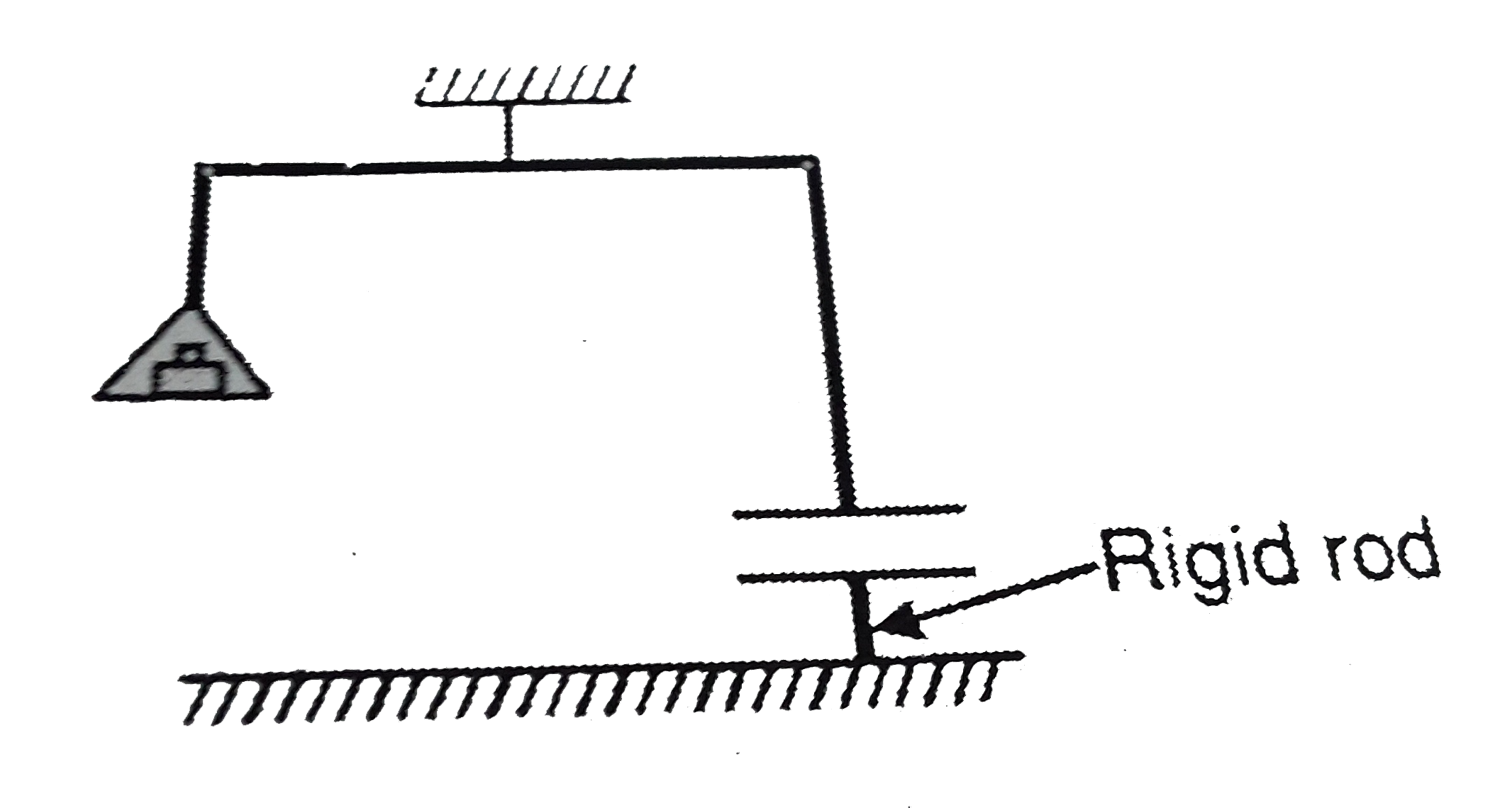
View SolutionThe lower plate of a parallel plate capacitor is supported on a rigid rod. The upper plate is suspended from one end of a balance. The two plates are joined together by a thin wire and subsequently disconnected. The balance is then counterpoised. Now a voltage V = 5000 volt is applied between the plates. The distance between the plates is d = 5 mm and the area of each plate is A =100cm2. Then find out the additional mass placed to maintain balance. [All the elements other than plates are massless and nonconducting]
View Solution
