A direct current of 2 A and an alternating current having a maximum value of 2 A flow through two identical resistances. The ratio of heat produced in the two resistances will be
1:1
1:2
2:1
4:1
The correct Answer is:C
To solve the problem of finding the ratio of heat produced in two identical resistances when a direct current (DC) and an alternating current (AC) flow through them, we can follow these steps:
Step 1: Understand the formula for heat produced
The heat produced (H) in a resistor is given by the formula:
H=I2RT
where:
- I is the current,
- R is the resistance,
- T is the time for which the current flows.
Step 2: Calculate heat produced by the direct current (DC)
For the direct current of 2 A:
- The current IDC=2A.
- The heat produced in the DC circuit is:
HDC=I2DCRT=(2)2RT=4RT
Step 3: Calculate heat produced by the alternating current (AC)
For the alternating current, we are given the maximum value of 2 A. The effective (RMS) value of the alternating current is given by:
IRMS=Imax√2=2√2=√2A
Now, we can calculate the heat produced in the AC circuit:
HAC=I2RMSRT=(√2)2RT=2RT
Step 4: Find the ratio of heat produced in DC to AC
Now we can find the ratio of heat produced in the two resistances:
Ratio=HDCHAC=4RT2RT=42=2
Thus, the ratio of heat produced in the two resistances is:
Ratio=2:1
Final Answer
The ratio of heat produced in the two resistances is 2:1.
---
The heat produced (H) in a resistor is given by the formula:
H=I2RT
where:
- I is the current,
- R is the resistance,
- T is the time for which the current flows.
For the direct current of 2 A:
- The current IDC=2A.
- The heat produced in the DC circuit is:
HDC=I2DCRT=(2)2RT=4RT
For the alternating current, we are given the maximum value of 2 A. The effective (RMS) value of the alternating current is given by:
IRMS=Imax√2=2√2=√2A
HAC=I2RMSRT=(√2)2RT=2RT
Now we can find the ratio of heat produced in the two resistances:
Ratio=HDCHAC=4RT2RT=42=2
Ratio=2:1
The ratio of heat produced in the two resistances is 2:1.
Topper's Solved these Questions
Similar Questions
A steady current of magnitude I and an AC current of peak value I are allowed to pass through identical resistors for the same time. The ratio of heat produced in the two resistors will be
View SolutionA direct current of 10 A is superimposed on an alternating current / = 40 cos ωt (A) flowing through a wire. The effective value of the resulting current will be
View SolutionA direct current of 5 amp is superimposed on an alternating current I=10sinωt flowing through a wire. The effective value of the resulting current will be:
View SolutionA direct current of 5 amp is superimposed on an alternating current I=10sinωt flowing through a wire. The effective value of the resulting current will be:
View SolutionThe current flowing in 3Ω Resistance will be
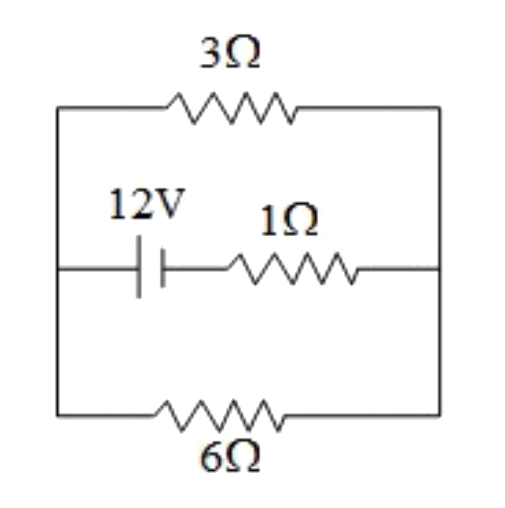
View SolutionA capacitor of capacitance C has charge Q. it is connected to an identical capacitor through a resistance. The heat produced in the resistance is
View SolutionTwo cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View SolutionIf a direct current of value a ampere is superimposed on an alternating current1=bsinωt flowing through a wire, what is the effective value of the resulting current in the circuit?
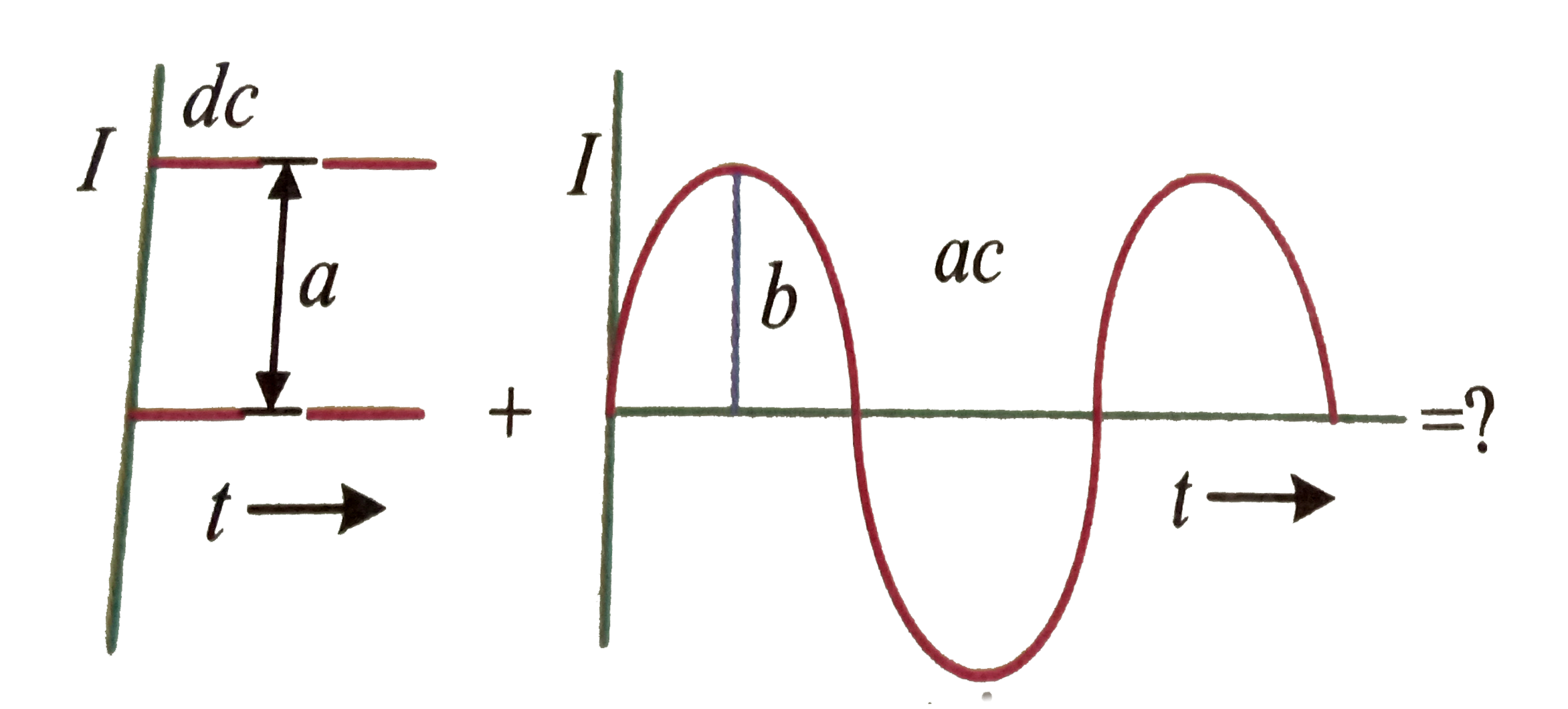
View SolutionIn a heating arrangement , an alternating current having a peak value of 28 A is used . To produce the same heat energy , If the constant current is used, its magnitude must be
View SolutionIf a direct current of value a ampere is superimposed on an alternative current I=b sinωt flowing through a wire, what is the effective value of the resulting current in the circuit?

View Solution
