A light beam, passes from medium 1 to medium 2. Show that the emerging beam is parallel to the incident beam.
The correct Answer is:A, C
To show that the emerging beam is parallel to the incident beam when a light beam passes from medium 1 to medium 2, we will use Snell's Law. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have two media: medium 1 (with refractive index μ1) and medium 2 (with refractive index μ2). A light beam is incident on the boundary between these two media at an angle i1.
Step 2: Apply Snell's Law at the First Interface
According to Snell's Law, when light passes from one medium to another, the relationship between the angles of incidence and refraction is given by:
μ1sin(i1)=μ2sin(r1)
where:
- i1 is the angle of incidence in medium 1,
- r1 is the angle of refraction in medium 2.
Step 3: Apply Snell's Law at the Second Interface
Now, when the light beam exits from medium 2 back into medium 1, we again apply Snell's Law:
μ2sin(r1)=μ1sin(i2)
where:
- i2 is the angle of incidence at the second interface (which is equal to the angle of emergence).
Step 4: Relate the Angles
From the two equations derived from Snell's Law, we can express r1 in terms of i1:
1. From the first equation:
sin(r1)=μ1μ2sin(i1)
2. Substitute this into the second equation:
μ2(μ1μ2sin(i1))=μ1sin(i2)
This simplifies to:
sin(i1)=sin(i2)
Step 5: Conclude that i1 = i2
Since the sine function is equal for the same angles, we conclude that:
i1=i2
This means that the angle of incidence at the first interface is equal to the angle of emergence at the second interface.
Step 6: Conclusion
Since both the incident ray and the emergent ray make the same angle (i1) with the normal, the emergent beam is parallel to the incident beam.
Final Statement
Thus, we have shown that the emerging beam is parallel to the incident beam when light passes from medium 1 to medium 2.
---
We have two media: medium 1 (with refractive index μ1) and medium 2 (with refractive index μ2). A light beam is incident on the boundary between these two media at an angle i1.
According to Snell's Law, when light passes from one medium to another, the relationship between the angles of incidence and refraction is given by:
μ1sin(i1)=μ2sin(r1)
where:
- i1 is the angle of incidence in medium 1,
- r1 is the angle of refraction in medium 2.
Now, when the light beam exits from medium 2 back into medium 1, we again apply Snell's Law:
μ2sin(r1)=μ1sin(i2)
where:
- i2 is the angle of incidence at the second interface (which is equal to the angle of emergence).
From the two equations derived from Snell's Law, we can express r1 in terms of i1:
1. From the first equation:
sin(r1)=μ1μ2sin(i1)
2. Substitute this into the second equation:
μ2(μ1μ2sin(i1))=μ1sin(i2)
This simplifies to:
sin(i1)=sin(i2)
Since the sine function is equal for the same angles, we conclude that:
i1=i2
This means that the angle of incidence at the first interface is equal to the angle of emergence at the second interface.
Since both the incident ray and the emergent ray make the same angle (i1) with the normal, the emergent beam is parallel to the incident beam.
Thus, we have shown that the emerging beam is parallel to the incident beam when light passes from medium 1 to medium 2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Example Type 101videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Example Type 113videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
A convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 10 cm apart with their principal axes coinciding. A beam of light travelling parallel to the principal axis and having a beam diameter 5.0 mm, is incident on the combination. Show that the emergent beam is parallel to the incident one. Find the beam diameter of the emergent beam.
View SolutionA beam of light passes from medium 1 to medium 2 to medium 3 as shown figure. What may be concluded about the three indices of refraction, n1,n2,andn3 ?
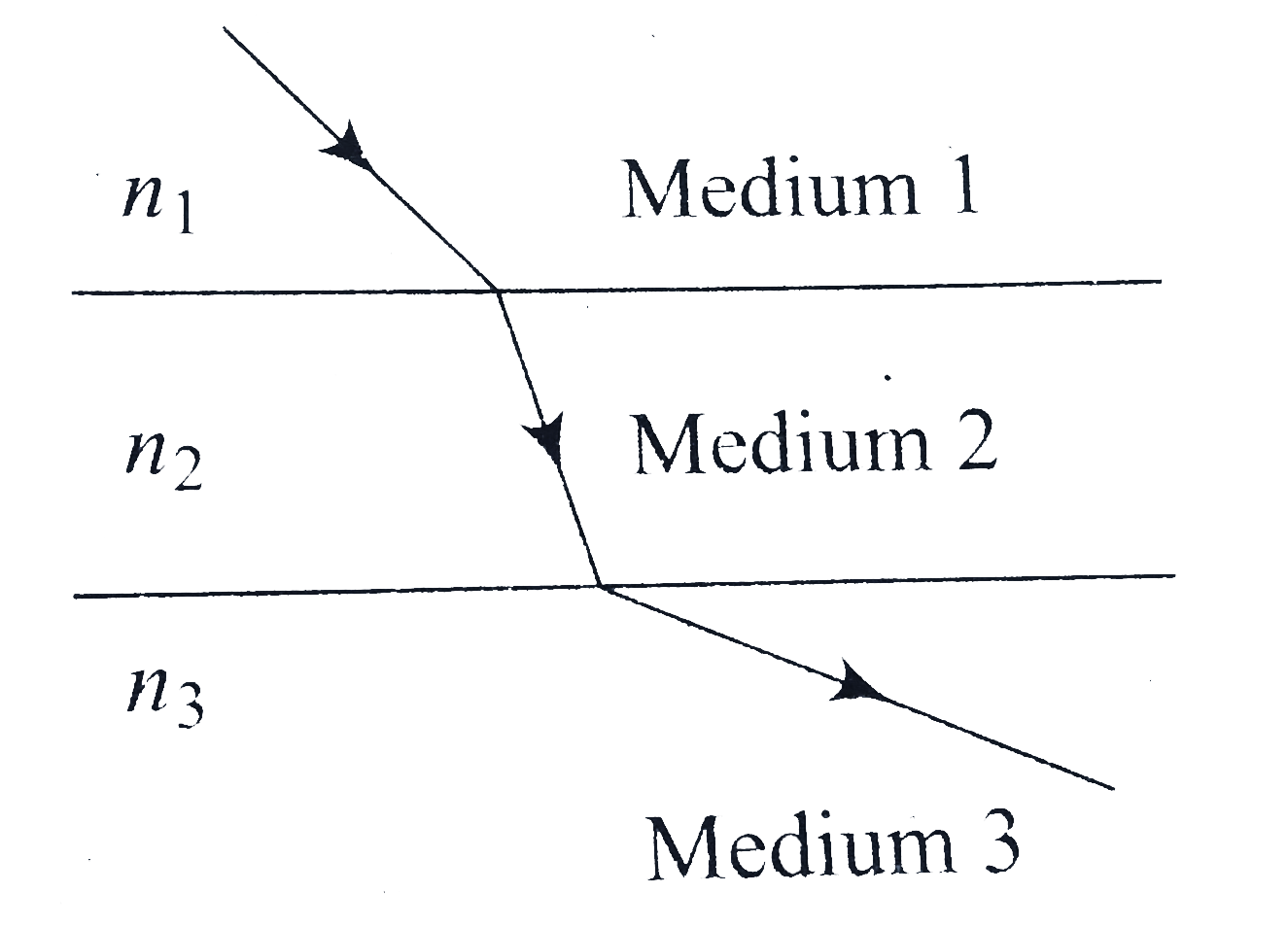 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A light ray does not bend at the boundary in passing from one medium to the other medium if the angle of incidence is :
A0∘B45∘C60∘D90∘
In the given figure, the faces of prism ABCD made of glass with a refractive index n form dihedral angles ∠A=90∘,∠B75∘,,∠C=135∘&∠D=60∘ (The Abbe's prism) .A beam of light falls on face AB & after total internal reflection from face BC escapes through face AD.Find the range of n and angle of incidence α of the beam onto face AB, if a beam that has passed through the prism in this mahner is perpedicular to the incident beam.
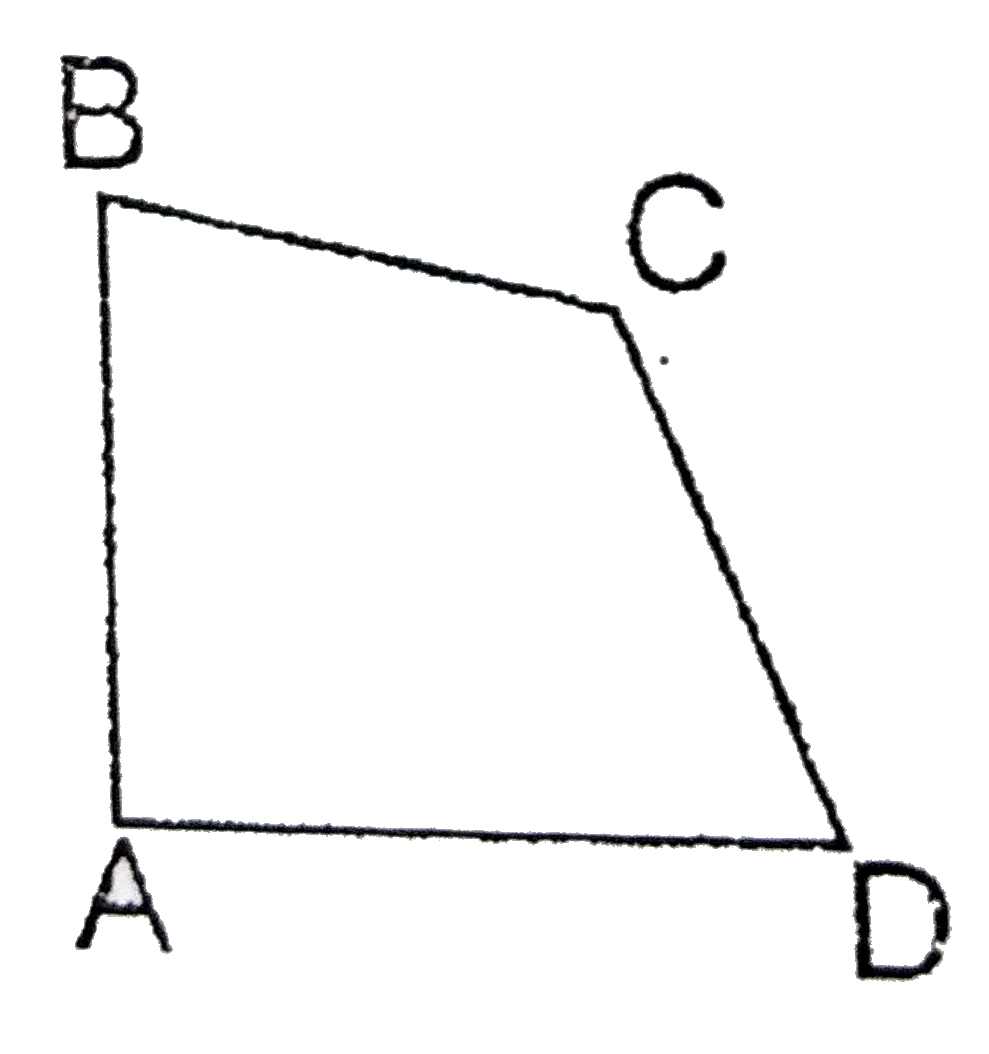 View Solution
View SolutionWhen a beam of light is incident on a plane mirror, it is found that a real image is formed. The incident beam must be
View SolutionWhen a beam of light goes from denser medium (μd) to rarer medium (μr), then it is generally observed that magnitude of angle of incidence is half that of angle of refraction. Then magnitude of incident angle will be-(here μ=μd/μr)
View SolutionA parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Show that if the incident beam makes an angle θ=sin−1(λ2d) with the normal to the plane of the slits, there will be a dark fringe at the centre Po of the pattern.
View SolutionA parallel beam of light falls normally on the first face of a prism of small angle .At the second face it is partly reflected,the reflected beam striking at the first face again, and emerging from it in a direction making an angle 6∘ 30' with the reversed direction of the incident beam. The refracted beam is found to have undergone a deviation of 1∘15' from the original direction.Find the refractive index of the glass and the angle of the prism.
View SolutionRefractive index of the material of concave lens is μ. The lens is immersed inb a medium of refractive index μ1(μ1>μ). A parallel beam of light is incident on the lens. Draw a diagram to show the path of emergent rays.
View SolutionSTATEMENT -1: A white parallel beam of light is incident on a plane glass-vacuum interface as shown. The beam may not undergo dispesion after suffering deviation at the interface (The beam is not incident normally on the interface.)

STATEMENT -2: Vacuum has same refractive index for all colours of white light.View Solution

